Solving Hex-Rays Challenge with Triton and TritonDSE

A few weeks ago, Robert Yates uploaded a tweet featuring a video solving a challenge by the company Hex-Rays with the use of Binary Ninja and the SENinja plugin. Inspired by this, I decided to embark on a similar journey, but this time using Triton and later incorporating TritonDSE. These two libraries provide powerful capabilities for Dynamic Symbolic Execution (DSE). Triton, written in C++, offers a Python API that makes it easy to work with. TritonDSE, on the other hand, is a Python library built on top of Triton, which provides DSE capabilities in a more accessible manner, along with other useful features such as program loading. For the disassembly and decompilation tasks, I will be using Ghidra, an open-source disassembler/decompiler written in Java and released by the NSA.
Authors
- Eduardo Blazquez
The Challenge
The challenge is an ELF binary for 64-bit architecture, dynamically linked, and has a size of 1.4 Mega bytes. We can obtain this information using the following command:
$ file challenge
challenge: ELF 64-bit LSB pie executable, x86-64, version 1 (SYSV), dynamically linked, interpreter /lib64/ld-linux-x86-64.so.2, BuildID[sha1]=83db7b297901c743a71f43e813e3dc266245b220, for GNU/Linux 3.2.0, stripped
$ ls -lah challenge
-rwxrwxr-x 1 symbolic symbolic 1.4M May 17 09:55 challenge
The program requires one argument to run, so we assume that it expects a specific flag or input. Our task is to find the correct flag to successfully execute the program. Let’s give it a try. When we run the program without providing any argument, we receive a message asking for a password. As an initial attempt, I’ll enter part of the name of a song by Rainbow: “Temple of the King”. Here’s what I got:
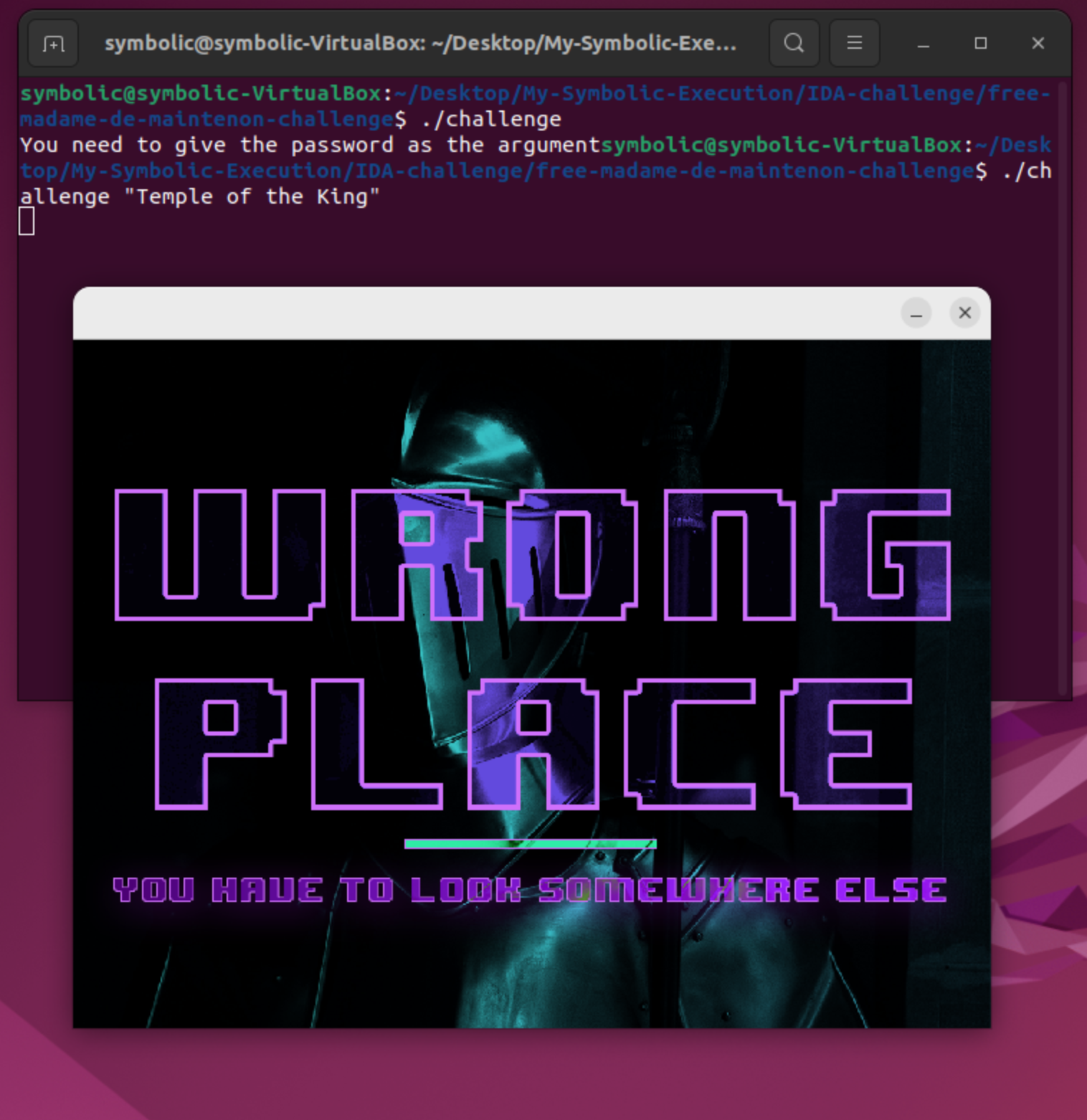
From the program’s output, we can see that it renders a PNG file, indicating that my initial approach was incorrect. It seems like I need to look for the password in a different place (or maybe the program just doesn’t appreciate Dio’s song…).
Instead of using other tools for analysis, I’ll directly open the binary in a disassembler. As mentioned earlier, I’ll be using Ghidra for this challenge.
Analyzing the Challenge with Ghidra
To analyze the binary using Ghidra’s disassembler and decompiler, we need to create a project in the tool. If you haven’t already done so, you can follow the instructions in the Ghidra documentation or refer to beginner’s tutorials to learn how to create a project (or if you want to dig deeper, I recommend you any of the next books Ghidra Software Reverse Engineering for Beginners, or The Ghidra Book: The Definitive Guide).
Once the project is created, we can load the binary into Ghidra. This can be done by selecting “File” -> “Import File” and choosing the binary file. Ghidra will analyze the binary and present you with the main project screen.
In the project screen, you will see various panels and tabs that provide different views of the disassembled code, decompiled code, and other program information. The main panel typically displays the disassembled code, and you can navigate through the different functions and sections of the binary.
To gain a better understanding of the code, we can use the decompiler view alongside the disassembler. The decompiler translates the assembly code into a higher-level language representation, making it easier to comprehend the logic of the program. You can switch to the decompiler view by selecting the appropriate tab or panel in Ghidra.
Using both the disassembler and decompiler views, we can examine the code, identify important functions or operations related to password handling, and trace the program’s execution flow.
It’s worth mentioning that while the decompiler provides a more readable representation, there may be cases where it struggles to accurately represent complex or obfuscated code. In such cases, referring back to the disassembled code can provide additional insights.
By carefully analyzing the disassembled and decompiled code, we can uncover the password validation mechanism and continue our journey to solve the challenge.
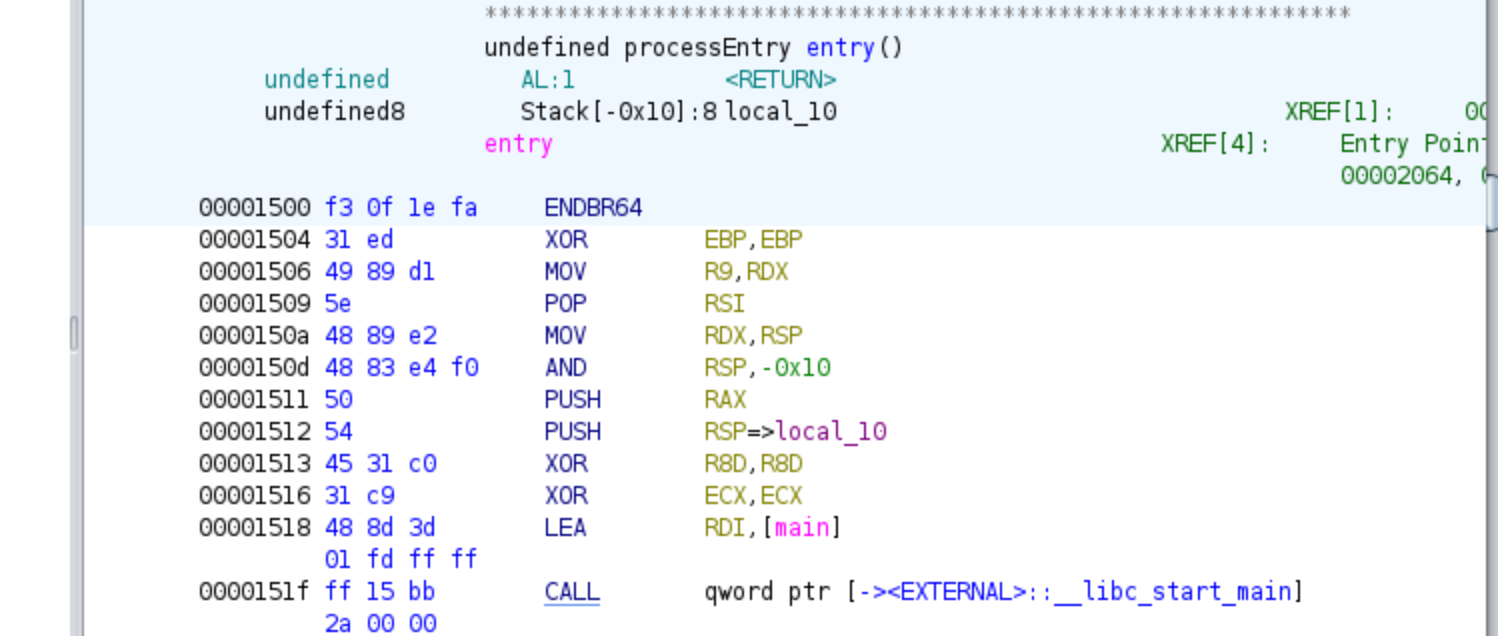
When we open the binary in Ghidra and click on it, Ghidra will automatically take us to the main function. The main function is typically the entry point of the program, where the execution starts.
However, if we were analyzing a binary where the entry point is not the main function, Ghidra would instead take us to the entry function. The entry function is a special function generated by the compiler and serves as the initial entry point specified in the ELF header (e_entry value).
In the entry function, we would usually see a call to the __libc_start_main function. The __libc_start_main function is part of the C runtime library and sets up the necessary environment for executing the program. The first argument (RDI register) passed to __libc_start_main is typically the address of the main function.
By following the function calls and analyzing the code, we can understand the flow of the program and identify the relevant parts for our analysis, such as the password validation logic or any other functionality we are interested in.
If we double click into the word main we will directly go to the main function, in my case I already renamed variables, and also I have changed the signature of the function, something you can do clicking on function’s name and pressing F.
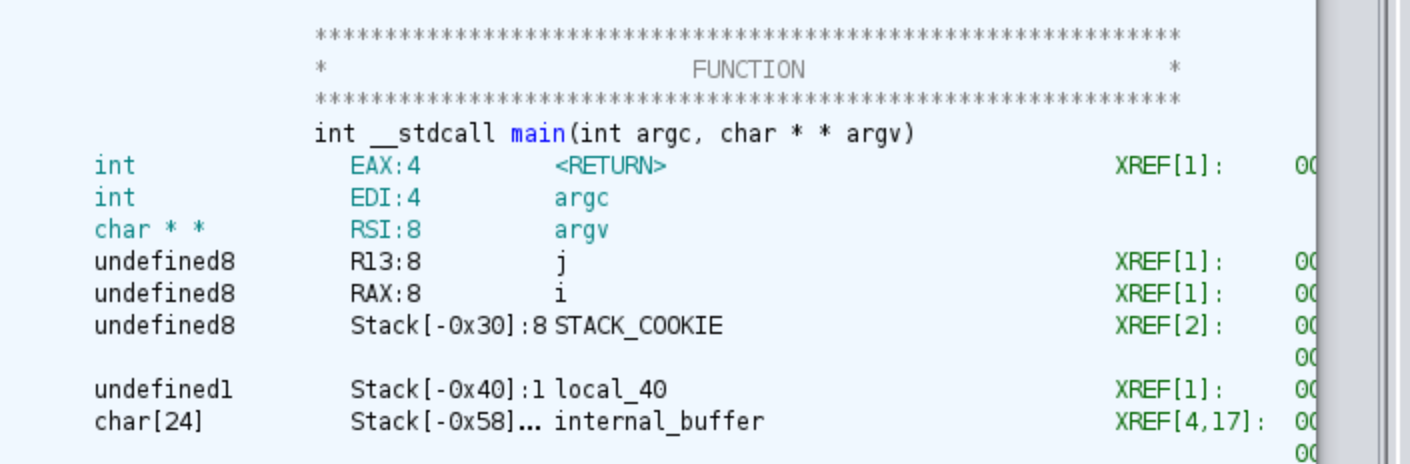
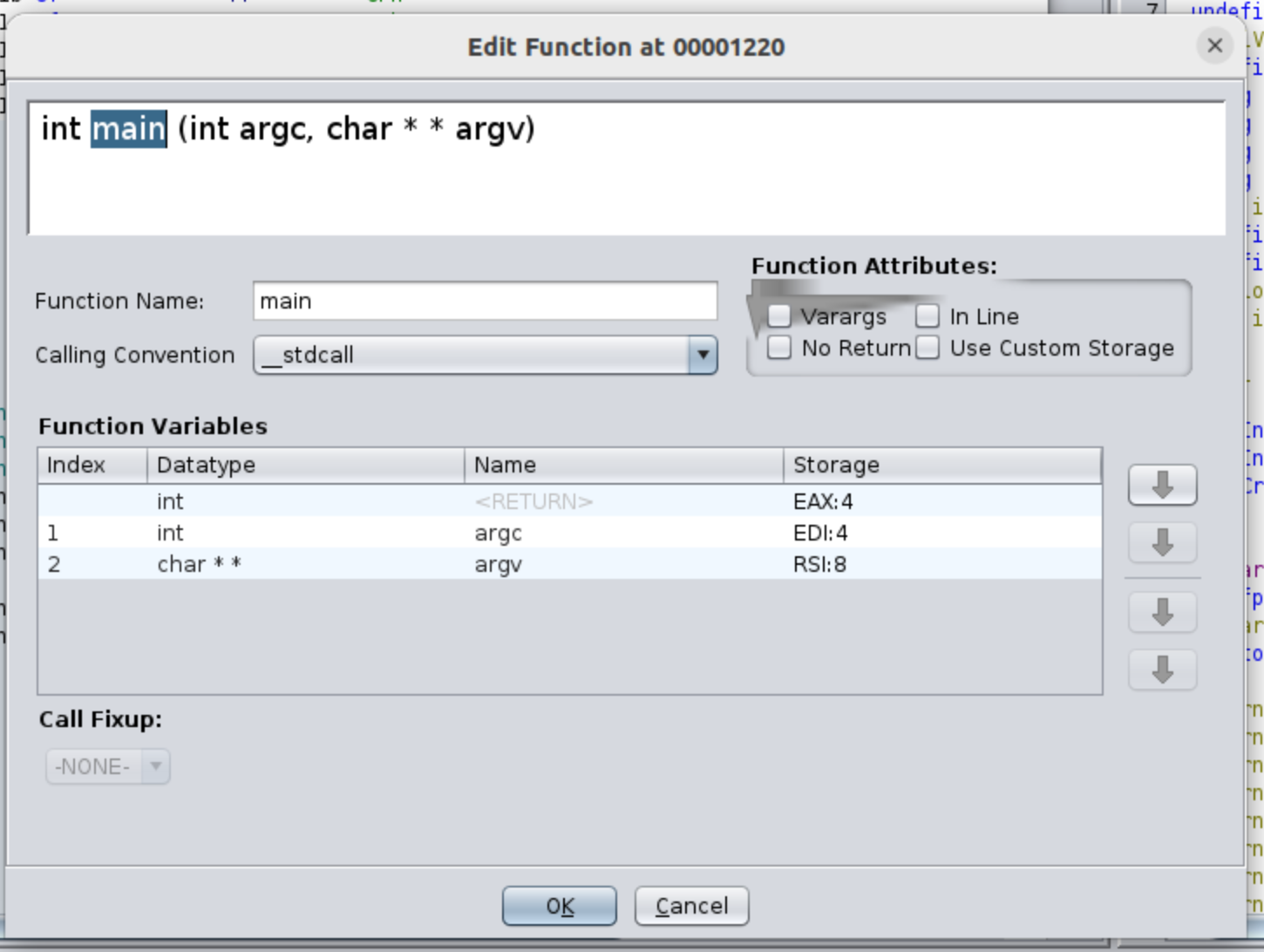
If later you want to rename variables remember that in Ghidra you have to click on variable’s name, and then press L, or for leaving a comment, you have to press ;.
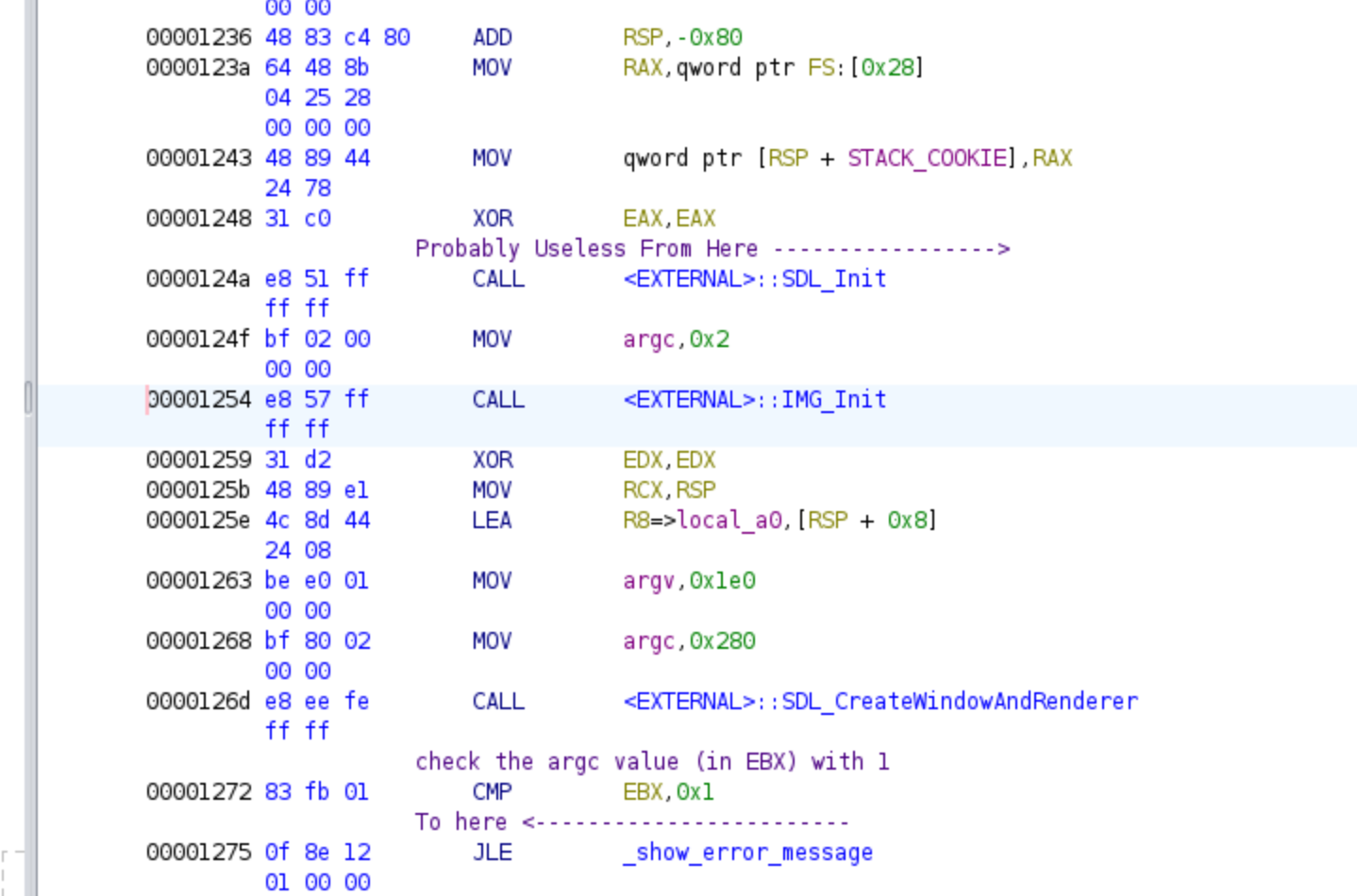
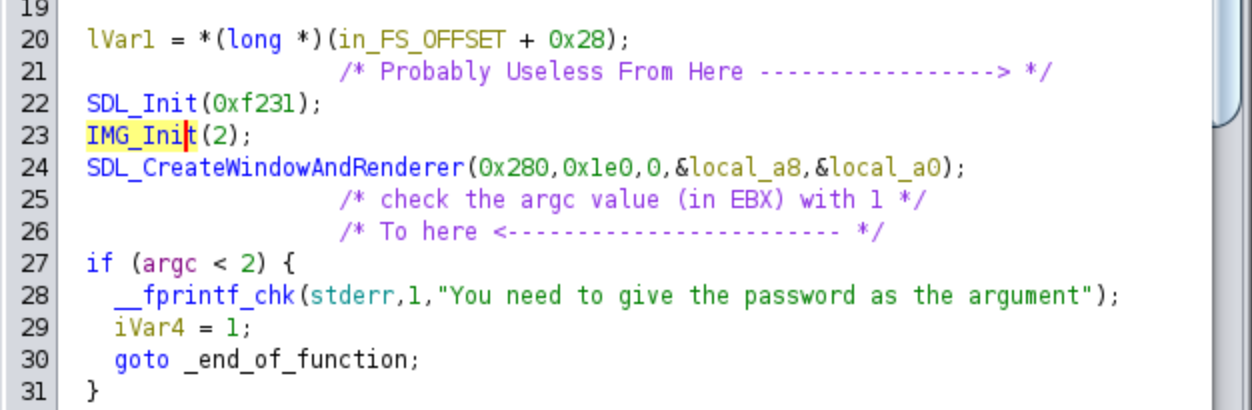
By skipping the prologue of the function, we are able to directly encounter a few calls to what appears to be the API of the SDL library. This library is utilized to provide access to hardware and graphics functionalities, making it particularly useful for rendering images and commonly employed in video games. Additionally, we observe the initial check of the argc value, ensuring that it is greater than 1. Otherwise, the program proceeds to the error code. Below, you’ll find both the assembly code and the decompiled code from Ghidra, accompanied by comments and renamed variables:
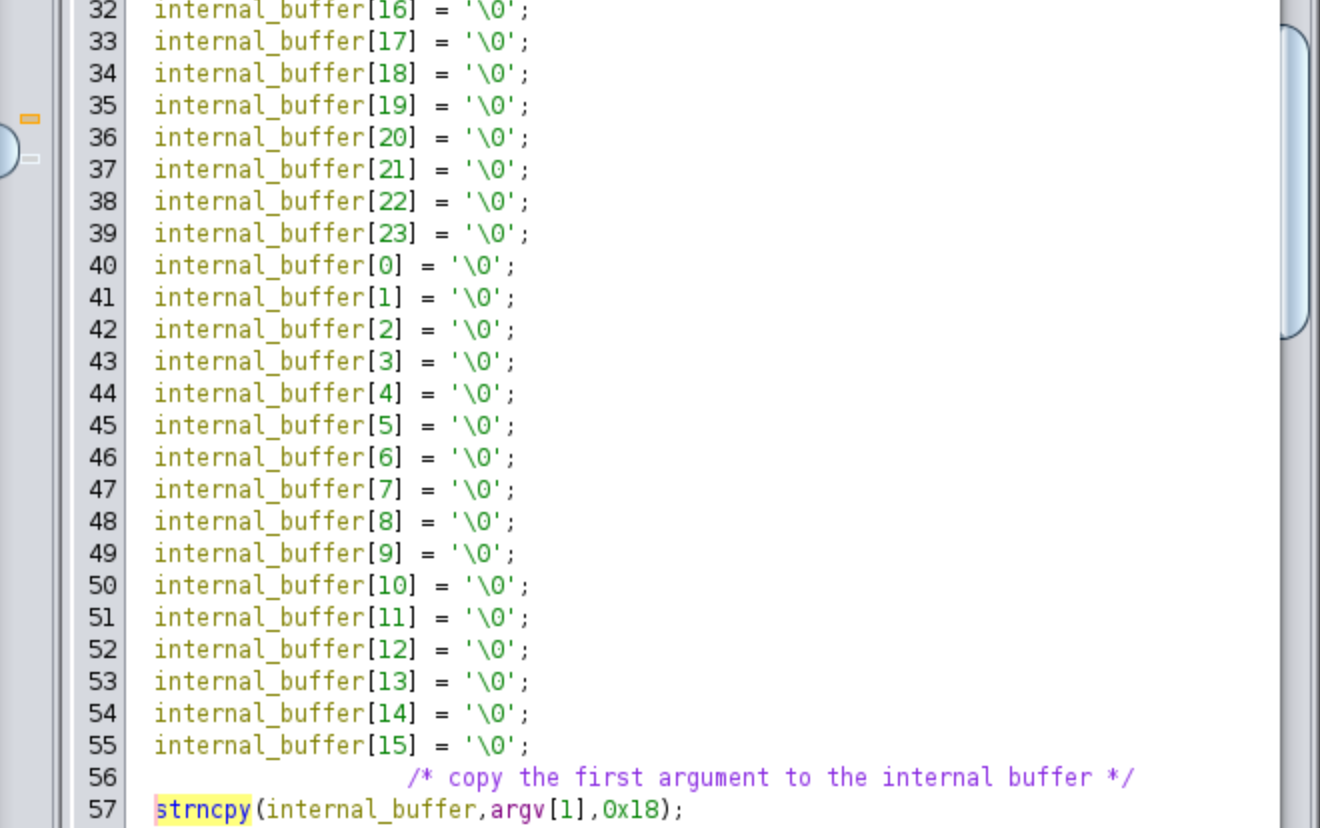
As we further analyze the code, we come across a section that is highly optimized in assembly, but in the pseudo-code representation provided by Ghidra, it appears to be the initialization of a large array. The code might have been generated using a memset function, but internally the compiler generates assembly code that utilizes the xmm0 register. This register is set to 0 using an xor operation and then used to initialize the first 16 bytes of a buffer. Additionally, we observe an initialization of byte 16 to 24 to 0. Finally, a call to strncpy is made, copying the contents from argv[1] to the initialized buffer. By considering these details, we can infer that this section is responsible for initializing a local buffer and copying the contents of argv[1] into it. In Ghidra, we can set the type of the buffer by pressing the ‘Y’ key and selecting the appropriate type. In my case, I chose the type uint[0x18]. We could even easily implement it in C:
int main(int argc, char **argv)
{
char internal_buffer[0x18];
...
memset(internal_buffer, 0, 0x18);
strncpy(internal_buffer, argv[1], 0x18);
}
But with Ghidra we will find something like the next:

Getting Started with the Mathematics
Given that I’m using a DSE engine with a solver like Z3, it’s likely that readers have already realized that this challenge involves solving mathematical equations. It’s important to note that attempting to solve these equations manually would be both time-consuming and extremely difficult. In this section, we will examine the various equations present in the program and attempt to represent them. Through this exploration, we will gain a deeper understanding of why these equations play a crucial role in solving the challenge.
Equation 1
Following the strncpy call, we encounter the first equation that needs to be solved. Additionally, these initial constraints will be used to provide input to Z3, ensuring the challenge is correctly solved. The following images depict the first equation:


We have the first equation with the first constraint in this pseudo code:
Equation 2
So, we have established the first constraint, which means that Z3 needs to select values that fulfill the condition of obtaining the result 0x1cd4 for the previous operation.
Now, let’s move on to the second equation and the corresponding constraint, which is located right below the previously discussed code.


Let’s represent as I did before, the equation with a more mathematical notation:
Again, once we feed Z3 with this constrait, it will have to find another 4 values (again 8 bytes, because each value are word size) which solve the equation. In case any of the previous equations do not work, we will go to a code that will render the error PNG, and will apply a cleanup:
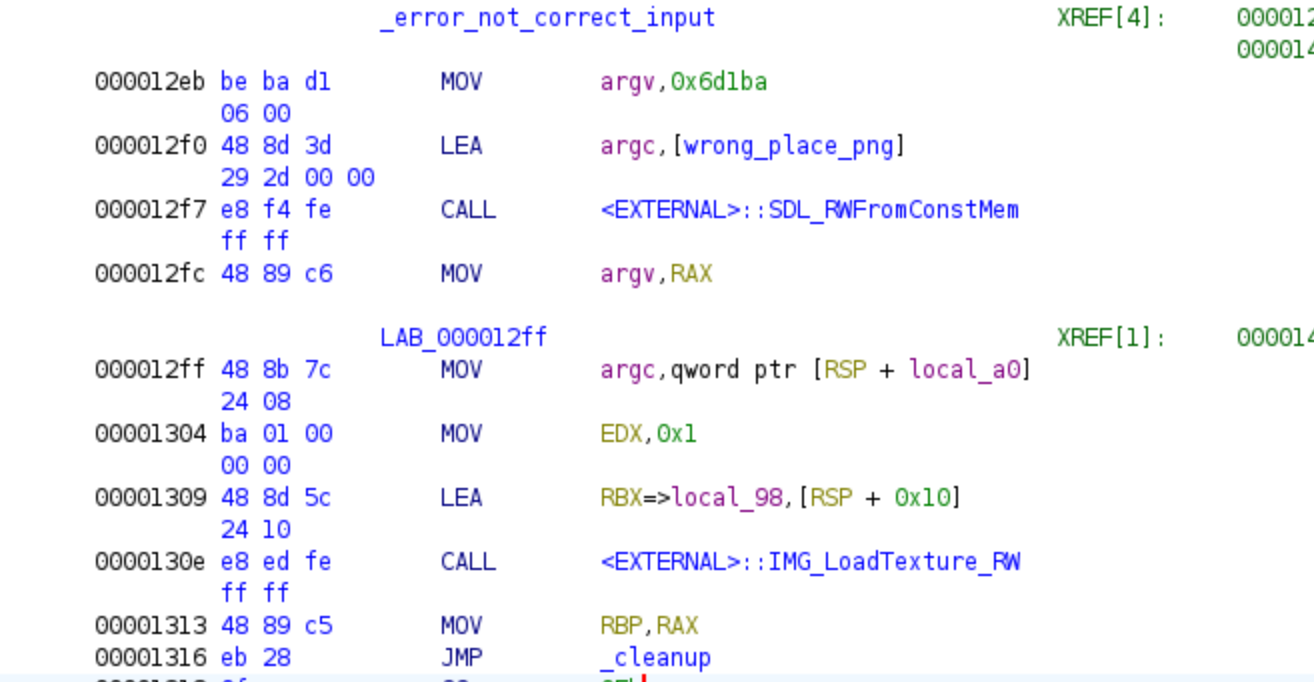
Equation 3 and first decryption loop
We will move following the JZ instruction and we can see the third equation:
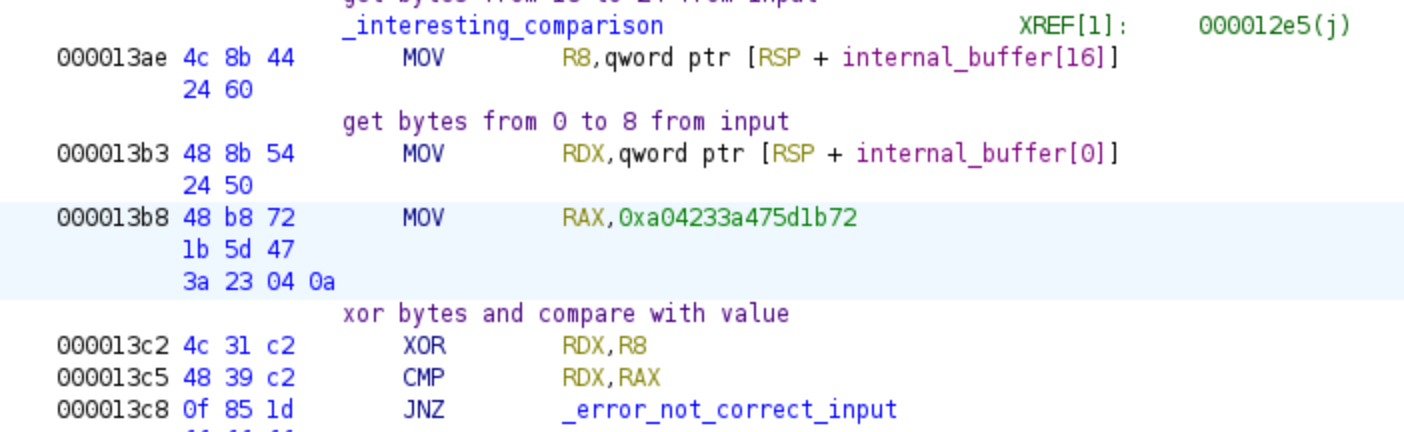
We obtain the next equation in a mathematical notation:
Once again, we will utilize this equation as a constraint for the bytes used by Z3. If this condition is not satisfied, the program would branch to the error code. However, if we provide the correct values, we would enter the first decryption loop.
The challenge includes an encrypted PNG file that will be decrypted using the provided password. Even if we attempt to bypass the jump instructions without correctly solving the challenge, we will not obtain the correct PNG. Assuming we have reached this point without bypassing any jumps and have provided the correct password so far, we will encounter the following code:
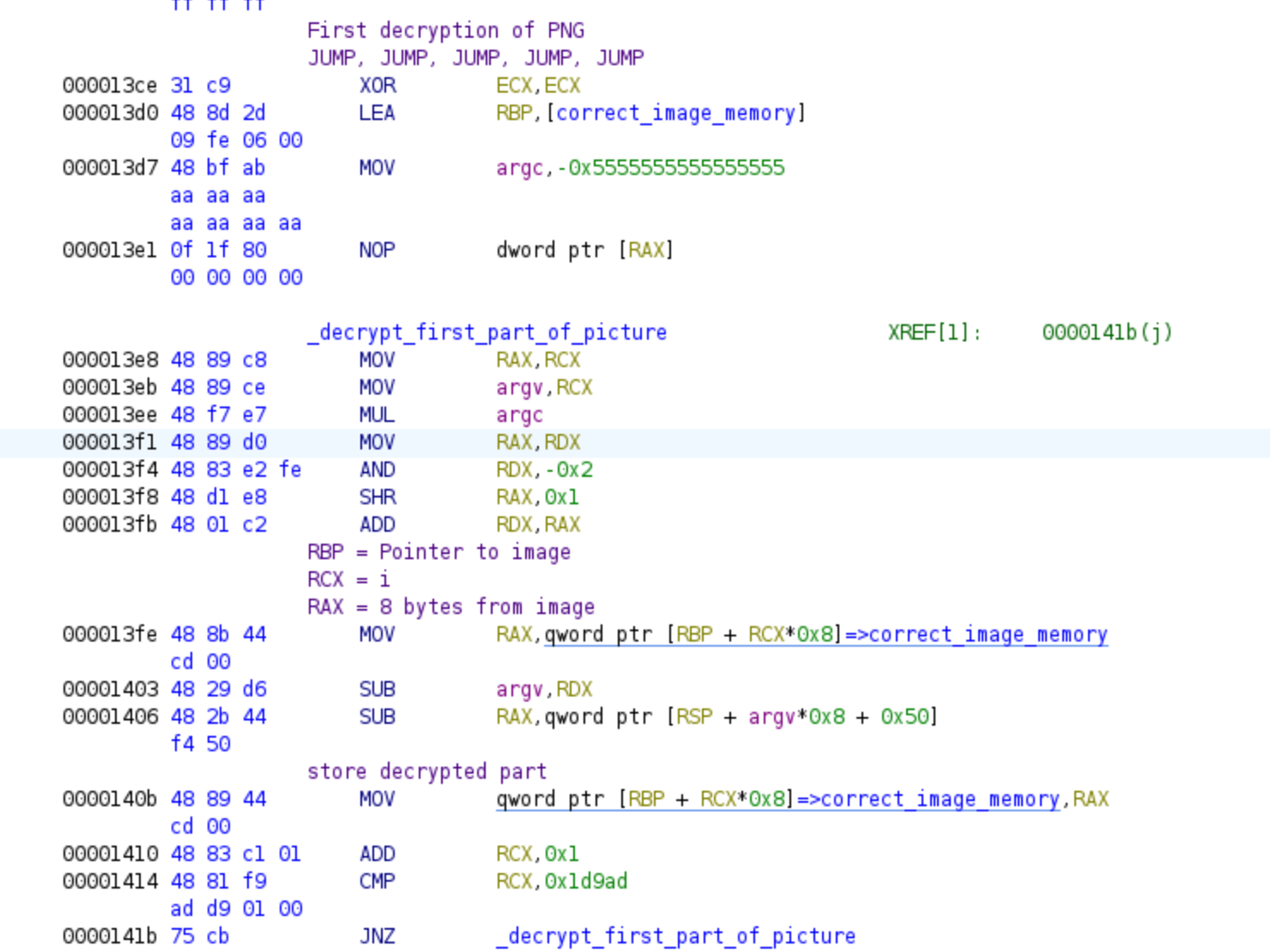
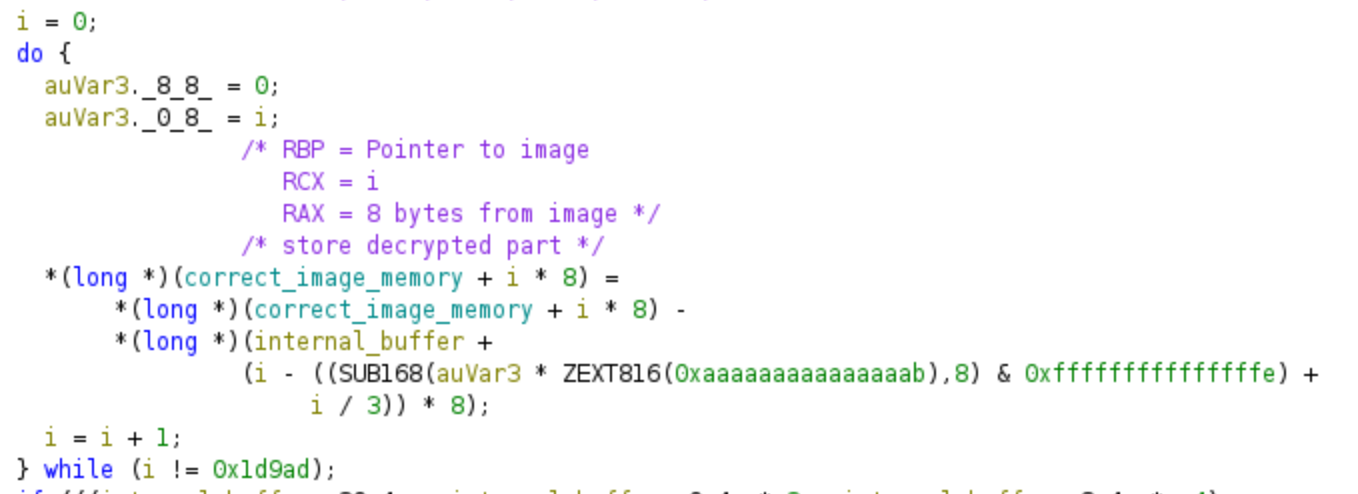
Although Ghidra is capable of generating decompiled code, it may appear somewhat unconventional and involve complex mathematical operations. In this case, I suggest referring to the assembly code, which tends to be clearer. The algorithm consists of a loop that performs a decryption operation using a portion of our password as the key. This aspect of the challenge makes it more difficult, as we need to find the correct password that successfully decrypts the PNG file. It’s important to remember the addresses of the decryption loop, as it is not relevant for symbolic execution, and bypassing it will save time and memory!
Equation 4 and second decryption loop
Once we step out the first decryption loop, we will have the fourth equation in the code, we can see its assembly and its pseudo-C in the next pictures:
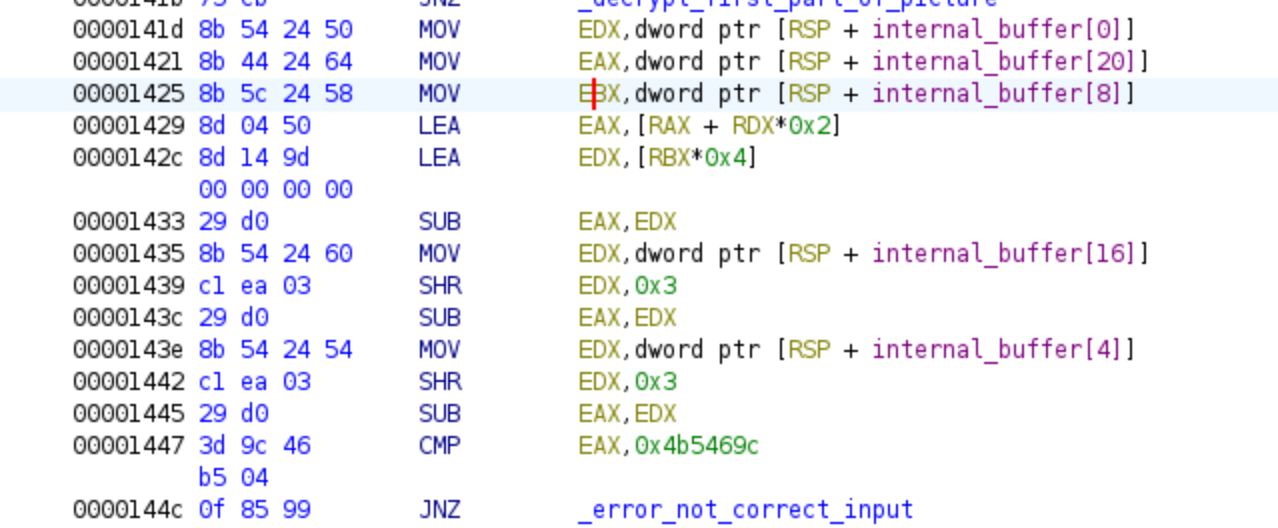

Once again, we will use this equation as a constraint for Z3 to derive additional portions of the password and ultimately obtain the correct password. Here is the equation used in this section of the code:
Similarly to the previous sections, if the computation using the provided password does not yield the value 0x4b5469c, we will be redirected to the error code, which displays an error PNG. However, if the correct password is supplied, we will directly jump to the second decryption loop.
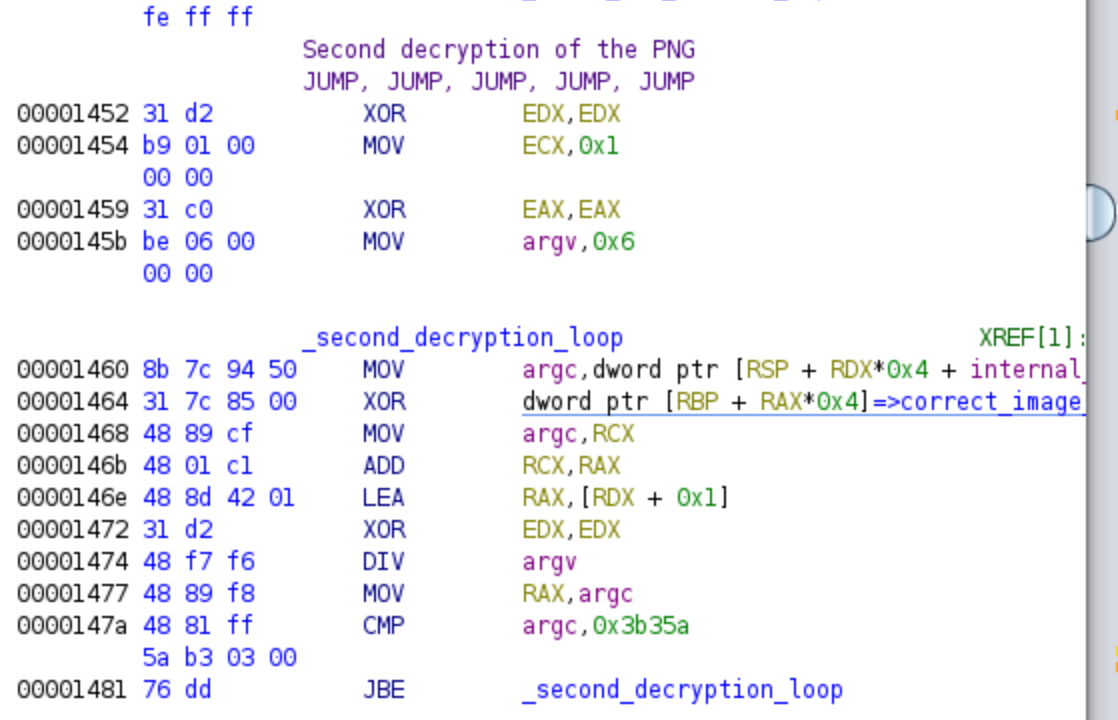

Again we have a decryption loop that uses the provided password from the user for decrypting the correct PNG. Again we would be working with a symbolic variable (I’ll show it in Triton’s part), for that reason what we will do is just step out and jump over this decryption loop. Keep these addresses too for the symbolic execution.
Last Equation
Once we have finished the second decryption loop we arrive to the final check applied in the program, this will be the last constraint our solver will need for obtaining the password, in the next pictures we can see the last equation, while we cannot see where R8 comes from and which value is used in the assembly, in the decompiled part we can see what addresses are xored.
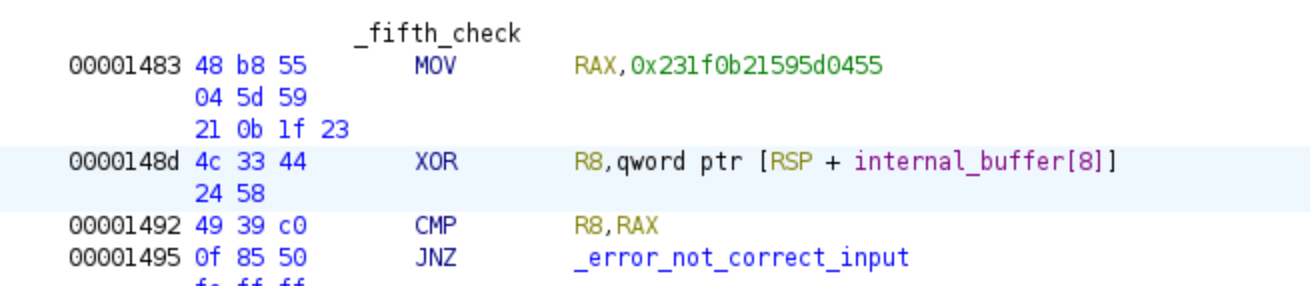
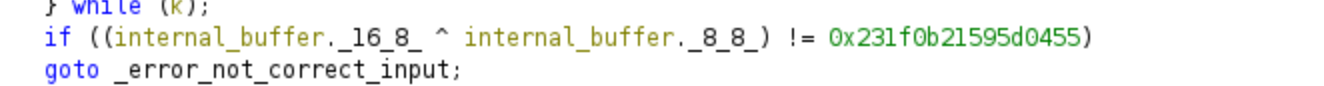
And here in a mathematical format as before:
With this part we would have finished the analysis of the equations and the constraints, we just leave from the program the next code:
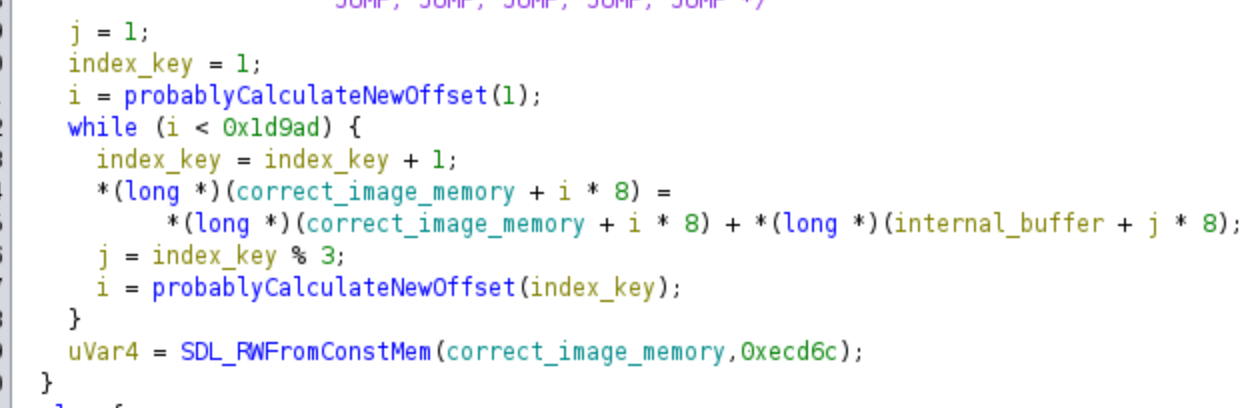
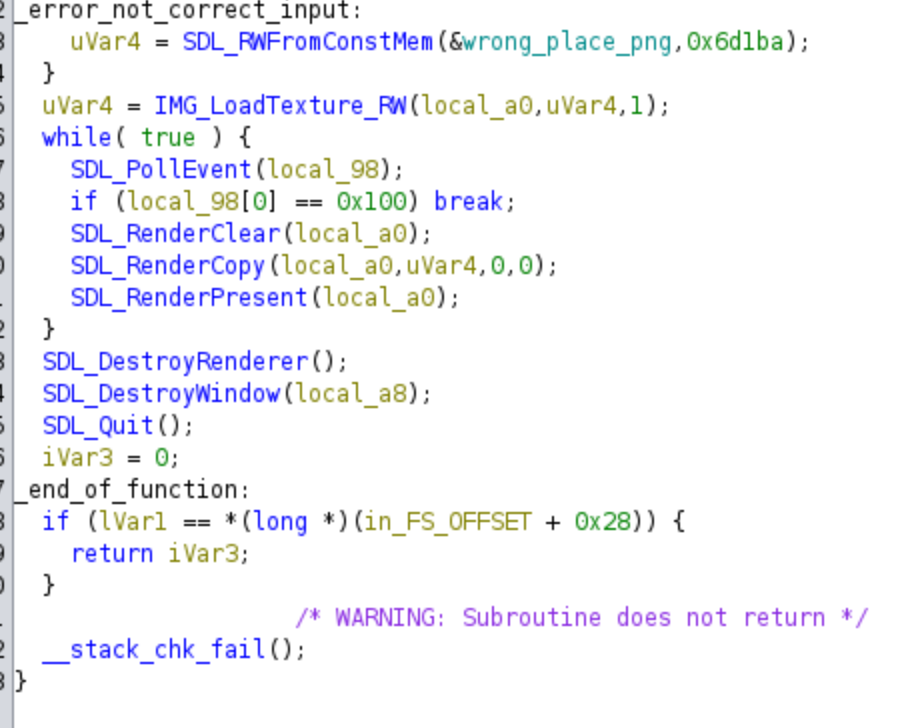
This part of the code just apply a final decryption, and finally it shows the image to the user, so we do not need to know anything more from the challenge for solving it.
Here are all the equations combined:
(password[6:8] + password[2:4] + password[20:22]) - password[10:12] = 0xd899
password[16:24] ⊕ password[0:8] = 0xa04233a475d1b72
((password[0:4] * 2 + password[20:24]) - (password[8:12]*4)) - (password[16:20] >> 3) - (password[4:8] >> 3) = 0x4b5469c
password[16:24] ⊕ passwords[8:16] = 0x231f0b21595d0455
These equations represent the constraints that need to be satisfied in order to find the correct password for the challenge. By solving these equations, we can obtain the values for the corresponding parts of the password that will successfully decrypt the PNG file.
Solving the Challenge With Triton

As stated on its website, Triton is a dynamic binary analysis library that provides internal components to build program analysis tools, automate reverse engineering, perform software verification, or emulate code.
The website also presents the architecture of Triton, which includes the following components:
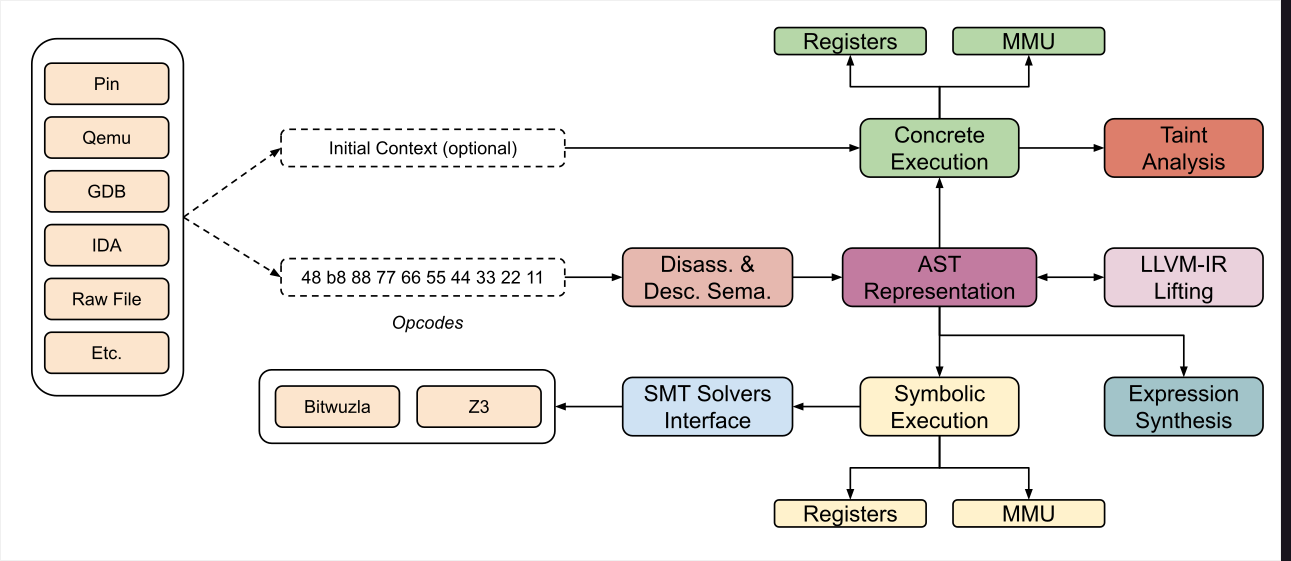
What we will do with Triton is emulate the code and set part of the memory as symbolic. When Triton runs the program’s code, it creates expressions using the symbolic variables, and we can retrieve an Abstract Syntax Tree (AST) representation from these expressions. We will apply different constraints to the expressions and use Z3 to solve them and obtain the password. The following steps will be followed:
- Create hooks for different library functions that are not implemented in Triton.
- Analyze the binary using Lief.
- Load the binary.
- Emulate the binary, applying library hooks and our own hooks.
- Apply constraints at specific points.
- Solve the final expression with the constraints.
In this part of the blog, I will include excerpts from the scripts. You can find the complete code of the script here.
Triton is primarily focused on analysis, so tasks like loading the binary, applying relocations, or allocating memory are not automatically handled by the library and are left to the analyst. The implementation of standard functions is also the analyst’s responsibility. However, Triton provides examples of these functions on its website. In the following sections, we will explore some of these functions and then proceed with the code for solving the challenge.
Creating Hooks for Library Functions
First, let’s see how to create a hook for the function __libc_start_main, in this function we will provide the code for giving the arguments to the program, the next code will be used in almost all the Triton scripts:
def libc_start_main(ctx):
print('[+] __libc_start_main hooked')
# Get arguments
main = ctx.getConcreteRegisterValue(ctx.registers.rdi)
# Push the return value to jump into the main() function
ctx.setConcreteRegisterValue(ctx.registers.rsp, ctx.getConcreteRegisterValue(ctx.registers.rsp)-CPUSIZE.QWORD)
# set as return value the address of main
# avoid all the libc stuff
ret2main = MemoryAccess(ctx.getConcreteRegisterValue(ctx.registers.rsp), CPUSIZE.QWORD)
ctx.setConcreteMemoryValue(ret2main, main)
# Setup argc / argv
ctx.concretizeRegister(ctx.registers.rdi)
ctx.concretizeRegister(ctx.registers.rsi)
# here write all the needed arguments
argvs = [
bytes(TARGET.encode('utf-8')), # argv[0]
b'A'*0x18 + b'\00'
]
# Define argc / argv
base = BASE_ARGV
addrs = list()
# create the arguments
index = 0
for argv in argvs:
addrs.append(base)
ctx.setConcreteMemoryAreaValue(base, argv+b'\x00')
base += len(argv)+1
print('[+] argv[%d] = %s' %(index, argv))
index += 1
# set the pointer to the arguments
argc = len(argvs)
argv = base
for addr in addrs:
ctx.setConcreteMemoryValue(MemoryAccess(base, CPUSIZE.QWORD), addr)
base += CPUSIZE.QWORD
# finally set RDI and RSI values
ctx.setConcreteRegisterValue(ctx.registers.rdi, argc)
ctx.setConcreteRegisterValue(ctx.registers.rsi, argv)
return (CONCRETE, 0)
We will also create a hook for the strncpy function. This function is used to copy the argument argv[1] into a local buffer in the stack, which represents the password provided by the user. Since we want to calculate this buffer, we will set it as symbolic. This will allow us to apply symbolic execution and obtain the different expressions associated with it.
def strncpy(triton_ctx):
global MEM_ADDRESS_BUFFER
print("[+] strncpy hooked")
# get rdi the first argument to be hooked
rdi = triton_ctx.getConcreteRegisterValue(triton_ctx.registers.rdi)
print("Symbolizing the user input in the address 0x%08X" % rdi)
# save the value
MEM_ADDRESS_BUFFER = rdi
# because we want the password to have only ASCII values,
# retrieve the minimum possible value
# and the maximum value
valid_characters = "0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ!\"#$%&\'()*+,-./:;<=>?@[\\]^_`{|}~"
min_value = ord(min(valid_characters))
max_value = ord(max(valid_characters))
for i in range(0x18):
memory_byte = MemoryAccess(rdi+i, CPUSIZE.BYTE)
# set first a concrete value (concolic)
triton_ctx.setConcreteMemoryValue(memory_byte, 61)
# symbolize the memory address for extracting the expression
triton_ctx.symbolizeMemory(memory_byte, "flag_%d" % (i))
# add the ascii string constraints
triton_ctx.pushPathConstraint(triton_ctx.getMemoryAst(memory_byte) >= min_value)
triton_ctx.pushPathConstraint(triton_ctx.getMemoryAst(memory_byte) <= max_value)
# finally set a 0 value (end of string)
triton_ctx.setConcreteMemoryValue(MemoryAccess(rdi+0x18, CPUSIZE.BYTE), 0)
# return the strncpy value as a concrete value
return (CONCRETE, 0x18)
HHere I have already added some constraints. Since we want a password with ASCII values, we will add two constraints for each value. The value must be greater than or equal to the minimum ASCII value for characters, and less than or equal to the maximum ASCII value for characters. To set the memory as symbolic, we use symbolizeMemory, and to create a constraint, we use pushPathConstraint. As symbolic execution can be computationally expensive, we concretize that memory with a concrete value, in this case, the value A. This technique is known as Concolic Execution.
Finally, we will have a structure that we will use to call these hooks, along with a function that will invoke the hooks during emulation. The code for this is as follows:
# the third value will be assigned during relocation.
customRelocation = [
['strncpy', strncpy, None],
['__libc_start_main', libc_start_main, None]
]
...
def hookingHandler(ctx):
'''
In case one of the run address is one from
the emulated functions, just call it and
get the result, check if it's needed to symbolize
the output register.
:param ctx: Triton's context for emulation.
'''
pc = ctx.getConcreteRegisterValue(ctx.registers.rip)
for rel in customRelocation:
if rel[2] == pc:
# Emulate the routine and the return value
state, ret_value = rel[1](ctx)
if ret_value is not None:
ctx.setConcreteRegisterValue(ctx.registers.rax, ret_value)
if state is SYMBOLIC:
print(f'[+] Symbolizing the return value')
ctx.symbolizeRegister(ctx.registers.rax)
# Get the return address
ret_addr = ctx.getConcreteMemoryValue(MemoryAccess(ctx.getConcreteRegisterValue(ctx.registers.rsp), CPUSIZE.QWORD))
# Hijack RIP to skip the call
ctx.setConcreteRegisterValue(ctx.registers.rip, ret_addr)
# Restore RSP (simulate the ret)
ctx.setConcreteRegisterValue(ctx.registers.rsp, ctx.getConcreteRegisterValue(ctx.registers.rsp)+CPUSIZE.QWORD)
return
Analyzing and Loading Binary
For obtaining binary structure, we will use Lief, a parser library that will allow us to obtain information like sections from the binary, relocations, and so on. Then we will load the binary into memory for doing the analysis. First, we will write some constants with the memory structure we want for the binary:
# Memory mapping
BASE_PLT = 0x10000000
BASE_ARGV = 0x20000000
BASE_STACK = 0x9ffffff0
ERRNO = 0xa0000000
Then we need a code that goes section by section loading the binary into memory:
def loadBinary(triton_ctx, lief_binary):
phdrs = lief_binary.segments
for phdr in phdrs:
size = phdr.physical_size
vaddr = phdr.virtual_address
print("[+] Loading 0x%06x - 0x%06x" % (vaddr, vaddr+size))
triton_ctx.setConcreteMemoryAreaValue(vaddr, list(phdr.content))
return
And finally, we need to apply relocations from the functions in the PLT, we will use the addresses from the imported functions to set the last values from customRelocation structure:
def makeRelocation(ctx, binary):
# Setup plt
print("[+] Applying relocations and extracting the addresses for the external functions")
for pltIndex in range(len(customRelocation)):
customRelocation[pltIndex][2] = BASE_PLT + pltIndex
relocations = [x for x in binary.pltgot_relocations]
relocations.extend([x for x in binary.dynamic_relocations])
# Perform our own relocations
for rel in relocations:
symbolName = rel.symbol.name
symbolRelo = rel.address
for crel in customRelocation:
if symbolName == crel[0]:
print('[+] Init PLT for: %s' %(symbolName))
ctx.setConcreteMemoryValue(MemoryAccess(symbolRelo, CPUSIZE.QWORD), crel[2])
break
return
Emulate the Binary
First of all we can create a run function that will initialize the stack registers (RBP and RSP) creating a fake stack, and that function will call the emulation one:
def run(triton_ctx, binary):
# define a fake stack
triton_ctx.setConcreteRegisterValue(triton_ctx.registers.rbp, BASE_STACK)
triton_ctx.setConcreteRegisterValue(triton_ctx.registers.rsp, BASE_STACK)
# Emulate binary from the entry point
print("[+] Starting emulation from entry point 0x%08X" % (binary.entrypoint))
d1 = time.time()
emulate(triton_ctx, binary.entrypoint)
d2 = time.time()
print("[+] Emulation finished.")
print("Time emulation: %.2f milliseconds" % ((d2-d1)*1000))
Finally, let’s take a look at the emulation function. This function follows the following process:
- It reads the opcodes from the memory pointed to by the current
program counterregister. - It disassembles the instruction.
- It tells Triton to apply the semantics of the instruction by calling its
processingfunction. - It advances the pointer to the next instruction.
Here is the code for the emulation function:
def emulate(ctx, pc):
# emulation loop
while pc:
opcodes = ctx.getConcreteMemoryAreaValue(pc, 16)
instruction = Instruction(pc, opcodes)
'''
You can insert some logic here
'''
# process the instruction
ret = ctx.processing(instruction)
# if HALT, finish the execution
if instruction.getType() == OPCODE.X86.HLT:
break
# apply one of the handlers that are not provided by
# Triton
hookingHandler(ctx)
# Next
pc = ctx.getConcreteRegisterValue(ctx.registers.rip)
Previous code represents a common emulation function for Triton, this body of function can be used almost in any analysis. Before moving to the next instruction we called hookingHandler, a function that will call our own hooks. I left a comment where we can insert some logic of analysis, apply symbolization of registers or memory, apply constraints and finally solve the expressions for getting a model.
Apply Constraints
Before I didn’t paste the whole code for emulate function, but I will paste here and I will give some explanations more:
def emulate(ctx, pc):
check_register_value = [
[FIRST_CONDITIONAL, ctx.registers.eax, 0x1cd4], # 0x000012bf
[SECOND_CONDITIONAL, ctx.registers.eax, 0xd899], # 0x000012e0
[THIRD_CONDITIONAL, ctx.registers.rdx, 0xa04233a475d1b72], # 0x000013c5
[FOURTH_CONDITIONAL, ctx.registers.eax, 0x4b5469c], # 0x00001447
[FIFTH_CONDITIONAL, ctx.registers.r8, 0x231f0b21595d0455] # 0x00001492
]
loop_address_dest = [
[FIRST_LOOP, 0x0000141d],
[SECOND_LOOP, 0x00001483]
]
# emulation loop
while pc:
#print("[-] Running instruction at address: 0x%08X" % (pc))
opcodes = ctx.getConcreteMemoryAreaValue(pc, 16)
instruction = Instruction(pc, opcodes)
# call a not implemented function, jump over it
# adding the length of a call instruction
if pc in [0x0000124a, 0x00001254, 0x0000126d]:
print("Not emulated function, continue")
pc = ctx.getConcreteRegisterValue(ctx.registers.rip)
pc += 5
continue
# avoid decryption loops
avoid_loop = False
for val in loop_address_dest:
if pc == val[0]:
print("Decryption loop address 0x%08X, moving to 0x%08X" % (val[0], val[1]))
pc = val[1]
avoid_loop = True
break
if avoid_loop:
continue
# conditions
for val in check_register_value:
if pc == val[0]:
print("Checking at address: 0x%08X" % (val[0]))
if pc == FIFTH_CONDITIONAL:
# in this case provide True for solving the expression
solver_check(ctx, val[1], val[2], True)
return
else:
solver_check(ctx, val[1], val[2])
# process the instruction
ret = ctx.processing(instruction)
# if HALT, finish the execution
if instruction.getType() == OPCODE.X86.HLT:
break
# apply one of the handlers that are not provided by
# Triton
hookingHandler(ctx)
# Next
pc = ctx.getConcreteRegisterValue(ctx.registers.rip)
First of all, as I said during the analysis of the binary, we will avoid two different codes, functions that are not implemented, and are not important for the analysis, we annotated the addresses of the calls, and we skipped them with the next code:
# call a not implemented function, jump over it
# adding the length of a call instruction
if pc in [0x0000124a, 0x00001254, 0x0000126d]:
print("Not emulated function, continue")
pc = ctx.getConcreteRegisterValue(ctx.registers.rip)
pc += 5
continue
Finally, let’s discuss another important part: the decryption loops. As mentioned before, we can actually avoid these decryption loops since they are not crucial for the analysis. Skipping them will help save time and memory during the symbolic execution.
# avoid decryption loops
avoid_loop = False
for val in loop_address_dest:
if pc == val[0]:
print("Decryption loop address 0x%08X, moving to 0x%08X" % (val[0], val[1]))
pc = val[1]
avoid_loop = True
break
if avoid_loop:
continue
For finishing explaining the code, we have the next snippet:
# conditions
for val in check_register_value:
if pc == val[0]:
print("Checking at address: 0x%08X" % (val[0]))
if pc == FIFTH_CONDITIONAL:
# in this case provide True for solving the expression
solver_check(ctx, val[1], val[2], True)
return
else:
solver_check(ctx, val[1], val[2])
This code will check the address, and it will call solver_check, in this function we will apply the constraints, the second parameter of the function is a register and the third parameter a value, both used for applying a constraint:
def solver_check(ctx, register, CHECK_VALUE, solve = False, show_ast = False):
# get the register AST
reg = ctx.getRegisterAst(register)
# add the constraint
ctx.pushPathConstraint(reg == CHECK_VALUE)
if show_ast:
# in case user wants, show the AST of the expression
ast = ctx.getAstContext()
reg_ast = ast.unroll(reg)
print(reg_ast)
...
# to meet the comparison, set the value of the register
# to the value checked.
ctx.setConcreteRegisterValue(register, CHECK_VALUE)
The previous code will apply the different constraints once the execution reach the different comparisons, and finally it will set the constant value into the register used in the comparison to keep running properly.
Solve the final expression with the constraints
We are almost done with Triton. In the solver_check function, I didn’t past some code that will execute if the solve parameter is set to True. This part of the code applies a final constraint, retrieves the expression from the Abstract Syntax Tree (AST), attempts to solve it using Z3, and obtains a model if successful.
if (solve):
# solve and retrieve the flag
cstr = ctx.getPathPredicate()
m = ctx.getModel(cstr)
key_values = {}
for k, v in m.items():
key_values[k] = v
flag = ""
for k in sorted(key_values.keys()):
v = key_values[k]
symbar = ctx.getSymbolicVariable(k)
#print(f"{symbar} ({k}) = {hex(v.getValue())} ({chr(v.getValue())})")
flag += chr(v.getValue())
print("\n\n------------------------------------------")
print(f"Flag={flag}")
print("------------------------------------------\n\n")
Using the previous code, we obtain the expression and attempt to obtain a model that satisfies the constraints. If we successfully obtain a model, we can retrieve the values for each variable in the solution. The obtained values may look something like this:
$ python3 triton_solver.py
...
flag_0:8 (0) = 0x46 (F)
flag_1:8 (1) = 0x72 (r)
flag_2:8 (2) = 0x33 (3)
flag_3:8 (3) = 0x33 (3)
flag_4:8 (4) = 0x5f (_)
flag_5:8 (5) = 0x4d (M)
flag_6:8 (6) = 0x34 (4)
flag_7:8 (7) = 0x64 (d)
flag_8:8 (8) = 0x61 (a)
flag_9:8 (9) = 0x6d (m)
flag_10:8 (10) = 0x33 (3)
flag_11:8 (11) = 0x2d (-)
flag_12:8 (12) = 0x44 (D)
flag_13:8 (13) = 0x65 (e)
flag_14:8 (14) = 0x2f (/)
flag_15:8 (15) = 0x4d (M)
flag_16:8 (16) = 0x34 (4)
flag_17:8 (17) = 0x69 (i)
flag_18:8 (18) = 0x6e (n)
flag_19:8 (19) = 0x74 (t)
flag_20:8 (20) = 0x65 (e)
flag_21:8 (21) = 0x6e (n)
flag_22:8 (22) = 0x30 (0)
flag_23:8 (23) = 0x6e (n)
But let’s printing it as a string, and will show it in a nice way :D
$ python3 triton_solver.py
[+] Loading 0x000040 - 0x000318
[+] Loading 0x000318 - 0x000334
[+] Loading 0x000000 - 0x000a88
[+] Loading 0x001000 - 0x001d11
[+] Loading 0x002000 - 0x0021d0
[+] Loading 0x003d28 - 0x15df4c
[+] Loading 0x003d38 - 0x003f48
[+] Loading 0x000338 - 0x000368
[+] Loading 0x000368 - 0x0003ac
[+] Loading 0x000338 - 0x000368
[+] Loading 0x002038 - 0x002084
[+] Loading 0x000000 - 0x000000
[+] Loading 0x003d28 - 0x004000
[+] Applying relocations and extracting the addresses for the external functions
[+] Init PLT for: strncpy
[+] Init PLT for: __libc_start_main
[+] Starting emulation from entry point 0x00001500
[+] __libc_start_main hooked
[+] argv[0] = b'./challenge'
[+] argv[1] = b'AAAAAAAAAAAAAAAAAAAAAAAA\x00'
Not emulated function, continue
Not emulated function, continue
Not emulated function, continue
[+] strncpy hooked
Symbolizing the user input in the address 0x9FFFFF80
Checking at address: 0x000012BF
Checking at address: 0x000012E0
Checking at address: 0x000013C5
Decryption loop address 0x000013CE, moving to 0x0000141D
Checking at address: 0x00001447
Decryption loop address 0x00001452, moving to 0x00001483
Checking at address: 0x00001492
------------------------------------------
Flag=Fr33_M4dam3-De/M4inten0n
------------------------------------------
Finally we obtain a password: Fr33_M4dam3-De/M4inten0n. Now let’s try running it as parameter for our challenge:
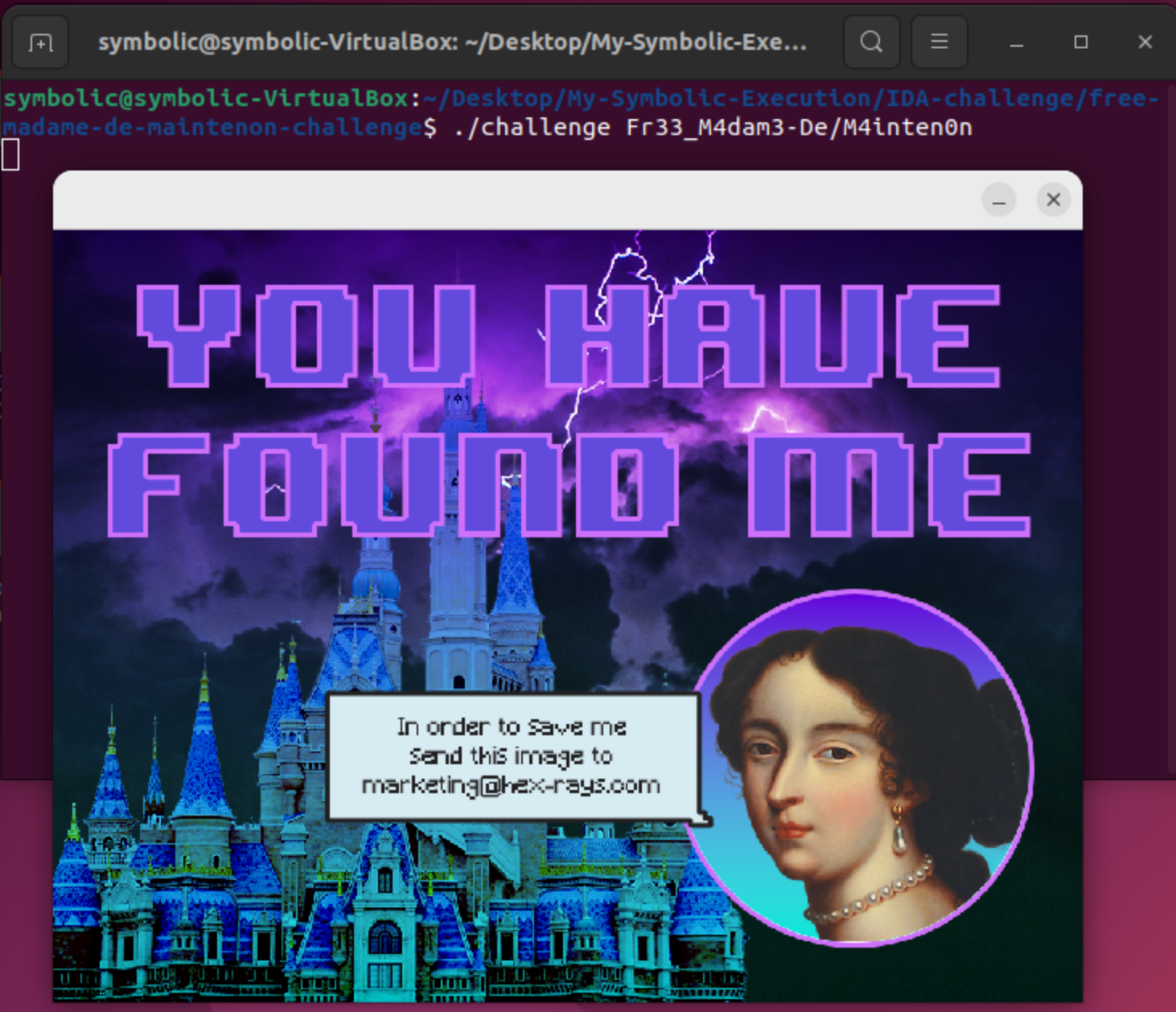
Solving the Challenge With TritonDSE
TritonDSE is a library built on top of Triton. It provides higher-level program exploration and analysis primitives, as stated in the Quarkslab post. It offers a callback manager that allows for the implementation of different hooking methods. TritonDSE includes a SymbolicExplorator that performs path exploration by generating new values to traverse the various branches of the code. Another advantage is that TritonDSE automatically loads the binary itself and already implements some API functions from libc, making the work of analysts easier.
Although the library was recently released and may still have some issues, it shows great promise for binary analysis. Unfortunately, due to time constraints, I wasn’t able to fully utilize TritonDSE for the challenge. Nonetheless, I will present my solution using TritonDSE and plan to enhance the script in the future as I learn more about it, aiming to solve the challenge in a more automated manner. For now, I will provide a simplified explanation in three steps:
- Load the binary (create initial values, set callbacks, and run the executor).
- Skip non-emulated functions and loops, and set byte constraints.
- Set constraints and solve the challenge.
Load Binary, configure starting values, configure callbacks and Run!
The process of loading the binary and configuring values or callbacks becomes much easier with TritonDSE as it abstracts many of the internal details of Triton. We load the binary by calling the Program function and providing the file path as an argument. Then, we can generate the program arguments as a Seed object, which will later be passed as a parameter to the SymbolicExecutor. The SymbolicExecutor object will load the Program object and also contains a callback_manager where we can register different callbacks. I recommend referring to the documentation to understand all the available callbacks. In my case, I only used one callback before each run instruction and one callback after running each instruction. Here is the main function from my script:
def main():
global p
# load the target into the engine
p = Program(TARGET)
# now generate the first seed values
config = Config(coverage_strategy=CoverageStrategy.PATH, debug=True,
pipe_stdout=True, seed_format=SeedFormat.COMPOSITE)
seed = Seed(CompositeData(argv=[b"./challenge", b"A"*0x18]))
# create a symbolic explorator to go
# symbolically over the program
executor = SymbolicExecutor(config, seed)
executor.load(p)
# set the callbacks for pre and post instruction
executor.callback_manager.register_pre_instruction_callback(trace_inst)
executor.callback_manager.register_post_instruction_callback(skip)
executor.run()
As you can see, the code is pretty straightforward, which is nice from an analysis perspective. We don’t need to write many lines of code to load a program and apply relocations, etc.
Skip not emulated functions, loops and set bytes constraints
I’ve found that if I try to skip a function in a pre callback, or in the hook of an API call, the program crashed or it didn’t work. In the case of the API calls, it crashes because the __default_stub function is called when a call to a not supported API is run, and the program tries to obtain an address using the program_counter, you can find the code here. But because in the hook of the API I modify the RIP register, the value accessed in Python’s map doesn’t exist and program crashes.
In my implementation, similar to how I handled Triton’s code, I have a mechanism to skip functions. I wait for the execution of the call instruction and then retrieve the return address stored in the RIP register. I also adjust the stack pointer RSP to clean up the stack. As for the decryption loops, I simply modify the RIP register and set it to the address following the decryption loop. After the strncpy call is completed, I apply ASCII constraints to each byte of the argv[1] value. The memory address of argv[1] is stored in the variable MEM_ADDRESS, and I will explain where this variable is written in the next section.
def skip(se: SymbolicExecutor, pstate: ProcessState, inst: Instruction):
pc = inst.getAddress()
if pc in [0x0000124a, 0x00001254, 0x0000126d]: # useless calls
print("[+] Not emulated function, continue")
# restore rip to a correct one
pstate.write_register(pstate.registers.rip, pc + inst.getSize())
# fix rsp
rsp = pstate.read_register(pstate.registers.rsp)
pstate.write_register(pstate.registers.rsp, rsp+8)
return
if pc == 0x000012a0: # post strncpy
valid_characters = "0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ!\"#$%&\'()*+,-./:;<=>?@[\\]^_`{|}~"
min_value = ord(min(valid_characters))
max_value = ord(max(valid_characters))
print("[+] strncpy adding constraints to symbolized memory")
# apply the constraint to the AST of each byte
for i in range(0x18):
sym_mem = pstate.read_symbolic_memory_byte(MEM_ADDRESS+i)
pstate.push_constraint(sym_mem.getAst() >= min_value)
pstate.push_constraint(sym_mem.getAst() <= max_value)
for value in loop_address_dest: # for stepping out the loops
if pc == value[0]:
print("[+] Found call to decryption loop, skipping")
pstate.write_register(pstate.registers.rip, value[1])
return
Set constraints and solve the challenge.
Finally, we have the callback that runs before each instruction. In this callback, I push various constraints into the expressions. Once we reach the final comparison, I push the last constraint and solve the challenge by searching for a model that satisfies all the expressions. As mentioned earlier, I also store the address of argv[1] in the MEM_ADDRESS variable. This is done during the strncpy call, where the address is one of the parameters.
def trace_inst(se: SymbolicExecutor, pstate: ProcessState, inst: Instruction):
global MEM_ADDRESS
pc = pstate.read_register(pstate.registers.rip)
...
if pc == 0x000012a0: # call to strncpy
rsi = pstate.read_register(pstate.registers.rsi)
print("[+] Strncpy getting source value: 0x%08X" % (rsi))
# save address of argv
MEM_ADDRESS = rsi
for value in check_register_value:
# go over the jumps of each check
# and apply the constraint with the used
# register.
if pc == value[0]:
print("[-] Found jump instruction, skipping it")
sym_reg = pstate.read_symbolic_register(value[1])
pstate.push_constraint(sym_reg.getAst() == value[2])
# to make sure the comparison always match
pstate.write_register(pstate.registers.zf, 1)
# Last constraint and solution of the system
if pc == FIFTH_CONDITIONAL:
print("[!] Got final instruction!")
sym_r8 = pstate.read_symbolic_register(pstate.registers.r8)
sym_rax = pstate.read_symbolic_register(pstate.registers.rax)
status, model = pstate.solve(sym_r8.getAst() == sym_rax.getAst())
# If formula is SAT retrieve input values
if status == SolverStatus.SAT:
# Retrieve value of the input variable involved in the cl value here (shall be only one here)
sym_mem = pstate.read_symbolic_memory_bytes(MEM_ADDRESS, 0x18)
var_values = pstate.get_expression_variable_values_model(sym_mem, model)
key_values = {}
for var, value in var_values.items():
key_values[var.getId()] = value
flag = ""
for k in sorted(key_values.keys()):
v = key_values[k]
flag += chr(v)
print("\n\n------------------------------------------")
print(f"Flag={flag}")
print("------------------------------------------\n\n")
sys.exit(0)
else:
print(status.name)
The structure check_register_value is pretty similar to the one shown in Triton’s part, and the code is similar too. In case the program counter value is one from check_register_value, we push a new constraint where the given register must be the same to the provided value, then we set ZF (zero flag) to 1, so the comparison will be true. Finally, if the address is the last condition, we push a final constraint and solve the expression as I did before.
If we run the script, we will get the next output:
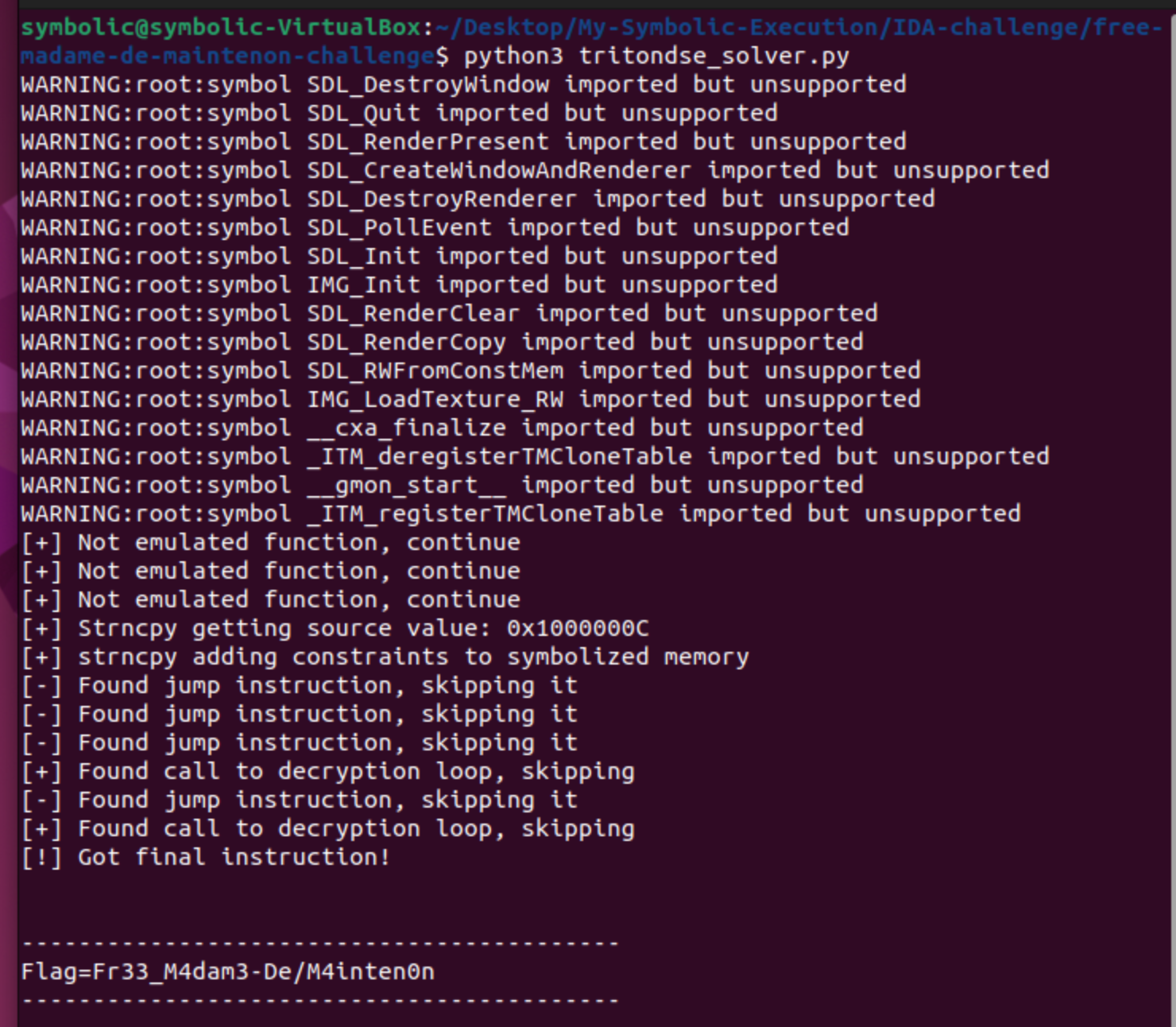
As we can see, the output is similar to the previous one from Triton’s script but with some logging code. Again we obtain the correct password, and running the challenge with the password will give us the same result. So with this we have finished with the part of TritonDSE!!!
You can find the full script for this challenge in here.
Using Z3 Together with Triton
This part will conclude the solution of the challenge, as a way to start learning about Triton. In this part of the post, I will use an external tool for solving the challenge, the script this time will directly use Z3, instead of calling it through Triton. The idea for this, as well as most of the code comes from the solution for HackCon2016 in Triton’s repository: script.
Internally Triton will use Z3 or Bitwuzla for solving the expressions, but you can directly use a tool like Z3 as a python library in the script. For using Z3 we need to prepare an expression in SMT format that Z3 can parse, and for doing that we will have two auxiliary functions:
def getVarSyntax(ctx):
s = str()
ast = ctx.getAstContext()
for k, v in list(ctx.getSymbolicVariables().items()):
s += str(ast.declare(ast.variable(v))) + '\n'
return s
def getSSA(ctx, expr):
s = str()
# current AST of the program
ast = ctx.getAstContext()
# generate an IR in SSA from the expression
ssa = ctx.sliceExpressions(expr)
for k, v in sorted(ssa.items())[:-1]:
s += str(v) + '\n'
s += str(ast.assert_(expr.getAst())) + '\n'
return s
In previous snippet we have two functions, getVarSyntax will generate all the variables for Z3 based on the symbolic variables from Triton, the output from the function is an string where each line has the next format:
(declare-fun <symbolic_var_N> () (_ BitVec <size in bits>))
The other function getSSA, will get the expression given as parameter, but this time in SMT format with Static Single-Assignment (SSA), this kind of representation is used in compilers’ IRs, where each variable is just assigned once. The format of the output is the next one:
(define-fun ref!269 () (_ BitVec 8) SymVar_8) ; Byte reference
(define-fun ref!271 () (_ BitVec 8) SymVar_9) ; Byte reference
(define-fun ref!281 () (_ BitVec 8) SymVar_14) ; Byte reference
(define-fun ref!283 () (_ BitVec 8) SymVar_15) ; Byte reference
(define-fun ref!285 () (_ BitVec 8) SymVar_16) ; Byte reference
(define-fun ref!287 () (_ BitVec 8) SymVar_17) ; Byte reference
(define-fun ref!297 () (_ BitVec 8) SymVar_22) ; Byte reference
(define-fun ref!299 () (_ BitVec 8) SymVar_23) ; Byte reference
(define-fun ref!300 () (_ BitVec 16) (concat ref!287 ref!285)) ; Extended part - Extended part - MOVZX operation
(define-fun ref!301 () (_ BitVec 32) ((_ zero_extend 16) ref!300)) ; Extended part - MOVZX operation
(define-fun ref!304 () (_ BitVec 16) (concat ref!299 ref!297)) ; Extended part - Extended part - MOVZX operation
(define-fun ref!305 () (_ BitVec 32) ((_ zero_extend 16) ref!304)) ; Extended part - MOVZX operation
(define-fun ref!308 () (_ BitVec 32) (bvadd ref!305 ref!301)) ; Extended part - ADD operation
(define-fun ref!317 () (_ BitVec 16) (concat ref!271 ref!269)) ; Extended part - Extended part - MOVZX operation
(define-fun ref!318 () (_ BitVec 32) ((_ zero_extend 16) ref!317)) ; Extended part - MOVZX operation
(define-fun ref!321 () (_ BitVec 32) (bvsub ref!308 ref!318)) ; Extended part - SUB operation
(define-fun ref!330 () (_ BitVec 16) (concat ref!283 ref!281)) ; Extended part - Extended part - MOVZX operation
(define-fun ref!331 () (_ BitVec 32) ((_ zero_extend 16) ref!330)) ; Extended part - MOVZX operation
(define-fun ref!334 () (_ BitVec 32) (bvsub ref!321 ref!331)) ; Extended part - SUB operation
(define-fun ref!343 () (_ BitVec 32) (bvsub ref!334 (_ bv7380 32))) ; CMP operation
(assert (= (ite (= ref!343 (_ bv0 32)) (_ bv1 1) (_ bv0 1)) (_ bv1 1)))
Now we can compare previous representation with the one from Triton, Triton represent the expression with an AST like the next:
(bvsub (bvsub (bvadd ((_ zero_extend 16) (concat flag_23 flag_22)) ((_ zero_extend 16) (concat flag_17 flag_16))) ((_ zero_extend 16) (concat flag_9 flag_8))) ((_ zero_extend 16) (concat flag_15 flag_14)))
While the input from Z3 can look longer, after talking with Jonathan Salwan (Main author from Triton), it looks like for long expressions Z3 parses faster the SMT expressions than Triton transforms from the AST to the expressions for Z3. So for some challenges where expressions are heavier to load, we can try using the method presented in this part of the post.
Now we need a function that interacts with Z3 library, this will create the symbolic expression to solve, and will generate the symbolic variables and the SSA form for Z3, find a solution for the expression, and in case some solution exists, return it for applying the concrete values to the symbolic variables:
def myExternalSolver(ctx, node, addr=None, debug=False):
import z3
expr = ctx.newSymbolicExpression(node, "Custom for Solver")
varSyntax = getVarSyntax(ctx)
ssa = getSSA(ctx, expr)
smtFormat = '(set-logic QF_BV) %s %s (check-sat) (get-model)' % (
varSyntax, ssa)
c = z3.Context()
s = z3.Solver(ctx=c)
s.add(z3.parse_smt2_string(smtFormat, ctx=c))
if addr:
print('[+] Solving condition at %#x' % (addr))
if s.check() == z3.sat:
ret = dict()
model = s.model()
for x in model:
if not "ref" in str(x):
ret.update(
{int(str(x).split('_')[1], 10): int(str(model[x]), 10)})
else:
continue
return ret
else:
print('[-] unsat :(')
sys.exit(-1)
return
In the previous code snippet, we create a symbolic expression from one of the parameters, this expression will be used to generate the SSA form. Then a string is created with the symbolic variables and the SSA expressions. This string in SMT format will be the input for Z3, for doing that we call parse_smt2_string, that will parse the string, and will generate the necessary constraints and expressions for Z3, and then we check if a solution can be found (comparison with z3.sat), in case a solution is found, we will retrieve the model that solves the system. I have found that sometimes the solution for the system includes the ref!... used as reference of the operation or reference of a symbolic variable in Z3, and when parsing the output the function will crash, since we find concrete values for symbolic variables, we will just skip them. In case of a symbolic variable, we will retrieve the name of the symbolic variable and a concrete value that solves the model.
Now, since we modified the solver function, we need to modify also the emulation function. This time we will just use a list to keep the addresses of the comparisons, and we will apply the check after processing the instruction, not before. Then we have the next emulation code:
def emulate(ctx, pc):
# This structure will be used for applying the constraints in certain
# addresses from the program, give a register to apply the constraint
# and the value used during the comparison.
check_register_value = [
FIRST_CONDITIONAL,
SECOND_CONDITIONAL,
THIRD_CONDITIONAL,
FOURTH_CONDITIONAL,
FIFTH_CONDITIONAL,
]
# Structure used to jump over the decryption loops which are
# not useful for the analysis
loop_address_dest = [
[FIRST_LOOP, 0x0000141d],
[SECOND_LOOP, 0x00001483]
]
# emulation loop
while pc:
# print("[-] Running instruction at address: 0x%08X" % (pc))
opcodes = ctx.getConcreteMemoryAreaValue(pc, 16)
instruction = Instruction(pc, opcodes)
# Code for stepping out code that is not necessary
# to be executed
# here avoid the loops and the functions that
# are not implemented
...
# process the instruction
ret = ctx.processing(instruction)
# if HALT, finish the execution
if instruction.getType() == OPCODE.X86.HLT:
break
# conditions
if pc in check_register_value:
print("Checking at address: 0x%08X" % (val[0]))
zf = ctx.getSymbolicRegister(ctx.registers.zf).getAst()
ast = ctx.getAstContext()
pco = ctx.getPathPredicate()
model = myExternalSolver(ctx, zf == 1, pc)
for k, v in list(model.items()):
ctx.setConcreteVariableValue(ctx.getSymbolicVariable(k), v)
# solve the equation and retrieve the whole Password
if pc == 0x0000149b:
# in this case provide True for solving the expression
ast = ctx.getAstContext()
pco = ctx.getPathPredicate()
print("Checking final at address: 0x%08X" % (pc))
mod = myExternalSolver(ctx, ast.land(
[pco] +
[ast.variable(ctx.getSymbolicVariable(x)) >= 0x20 for x in range(0, 0x18)] +
[ast.variable(ctx.getSymbolicVariable(x)) <= 0x7e for x in range(0, 0x18)] +
[ast.variable(ctx.getSymbolicVariable(x)) !=
0x00 for x in range(0, 0x18)]
))
serial = str()
for k, v in sorted(mod.items()):
serial += chr(v)
print("PASSWORD = %s" % (serial))
return
# apply one of the handlers that are not provided by
# Triton
hookingHandler(ctx)
# Next
pc = ctx.getConcreteRegisterValue(ctx.registers.rip)
If we find one of the addresses from the comparisons, we will call the external solver, giving as a symbolic expression the AST that is set in the ZF (zero flag) after the comparison, that must be equal to the value 1. This function will return symbolic variables and concrete values that solves the expression. We will apply them as concrete values. And we will continue the execution.
After that we have a comparison, that is already out of the different checks, it will be here we we will solve the final expression. In order to solve the final expression and obtain the correct values, we will retrieve as we did in the previous solution, the PathPredicate, and we will include also three constraints for our symbolic variables to be ASCII strings. Once we find a solution, this time we will obtain all the values for the symbolic variables. And with this, the correct password.
Next we can see the output with this script:
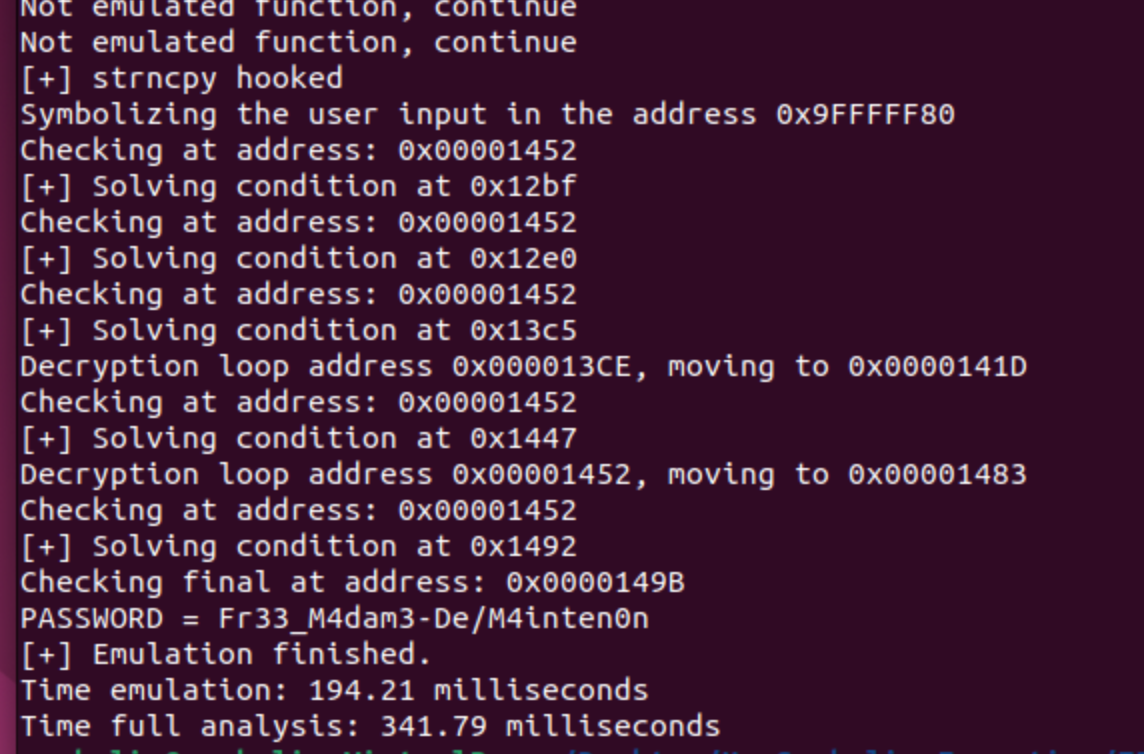
You can find the whole script here
Conclusions
I have found the challenge interesting and at the end not so difficult. From a reverse engineering point of view the binary is not hard to analyze, but the problem would be looking for solutions manually, or using brute force, or using other tools manually (we can solve this challenge writing a script for Z3 but this would take longer).
Regarding Triton or TritonDSE, I have found that while in both cases the documentation is a little bit “tough” to follow, but with a few examples and reading at same time documentation and source code, you can quickly write scripts useful for doing challenges like this, or even more difficult ones.
Finally I hope you enjoyed reading this post, this time it was a long post, but I think it was needed for understanding the challenge, and the process for solving it.
I want to thank Yates82 for his video solving the challenge with Binary Ninja, this video gave me the idea for doing the challenge using the covered tools and write the post. Also I want to thank JonathanSalwan, the main author of Triton, I think this tool is very useful and it offers a very high performance. And finally thank RobinDavid1 and Christian Heitman, authors of TritonDSE, I think this will make Triton more accessible, and easy to use, which will probably make more people using it.
See you Space Cowboy!
