Writing an IR from Scratch and survive to write a post
In this post, I will talk about the first version of the Intermediate Representation I designed for Kunai Static Analyzer, this is a dalvik analysis library that I wrote as a project for my PhD, also as a way of learning about the Dalvik file format and improving my programming skills.
Authors
Writer:
- Eduardo Blazquez
Technical and English reviewer:
Kunai Static Analyzer
Kunai was a static analysis library for dalvik bytecode. This library was published on Github, and it also was a paper published in the journal SoftwareX describing the projects and its benefits against another tool of the state of the art.
You can find the source code here: https://github.com/Fare9/KUNAI-static-analyzer
And the paper here: https://www.sciencedirect.com/science/article/pii/S2352711023000663
Although the project is discontinued (a new version is being written here Shuriken), I thought it would be interesting to write about my experience of how I wrote the first version of its Intermediate Representation (from now on IR), how I implemented the different algorithms, and how I transformed Dalvik bytecode into this IR.
As I said, this IR is the first version I wrote for Kunai, after that I decided to move my implementation to MLIR, an approach for writing specific IRs using a reusable and extensible compiler infrastructure. You can find my presentation of this new IR that I implemented, at EuroLLVM2023.
As I said, in this post I will dig into the process of creating an IR for supporting analysis of Dalvik Bytecode, the algorithms I followed and implemented, and finally the process for lifting the dalvik bytecode into this IR.
Please, grab a drink, play your favorite music (I recommend the following one if you want to chill: Dreamcatcher chill, or the next one if you prefer something with more rhythm: Dreamcatcher no ballad).
References
For the design and development of the IR I read chapters from different books, and I studied the code from different projects. Here you can find those books and projects:
Books
- Advanced Compiler Design & Implementation

- An Introduction to the Theory of Optimizing Compilers

- Compilers Principle, Techniques & Tools

- Introduction to Compilers and Language Design

- SSA-based Compiler Design

Projects
- LLVM
- Triton
- Miasm
- Redexer
- Soot
- Dexpler
- P-Code (An IR used in Ghidra)
- Binary Ninja IL
- Modern Binary Analysis with ILs
- Angr VEX IR
- Radare2 ESIL
MjolnIR - Kunai’s IR
My idea behind writing an IR for Kunai came from all the work I did during my PhD using Androguard. Many times using Androguard, I had to rely on the output of its disassembler and manually check the opcodes or even the mnemonic from the operation. While this process was easy for small analyses, it became hard for other projects. For example, I remember helping my friend Julien with one of his papers, at that moment we wanted to write a static taint analysis tool for Dalvik, and one of the ideas we had was to include a simple IR that would help us to recognize instructions in Androguard. It was at that moment when I saw the disadvantages of using Androguard, there was not a representation that could help us with the analysis (some time after that I discovered an Abstract Syntax Tree representation, but it is mostly used for the decompiler). After that, once I was writing Kunai, I thought that Kunai would benefit from an IR that would help analysts to write analyses with Kunai.
First of all, the most challenging decision choice was “what’s a cool name I can give it?”. Of course, a cool project needs a cool name. And because the project already had the name Kunai (a japanese farming tool popular for being the most used weapon in the manga/anime Naruto), the name of a weapon would be really cool as a name, and at that moment I remembered the following:

Mjölnir, the weapon of Thor, god of thunder in Norse Mythology. I had a cool name, and if I wrote it like MjolnIR, I could say that the last two characters come from Intermediate Representation.
Although the idea was good, my knowledge of the IRs was limited, and mostly based on using tools like Triton that gave me access to LLVM-IR code, or analyzing binaries using Ghidra and observing the generated P-code. Of course, I also remembered the little knowledge I gained in the Compiler’s class during the undergraduate bachelor in Computer Engineering. But I was willing to write the IR, and I had enough bibliography to start reading, as well as different projects to start learning from their code.

MjolnIR - Structure of an IR
Each Intermediate Representation or Intermediate Language can have its own shape, and own design. We can have that it is text-based or binary-based, or even a mix of both (for allowing modifications directly with a text-editor but fast processing with tools). We can have the next like Intermediate Representations (from the book Introduction to Compilers and Language Design) :
- Abstract Syntax Tree (AST): although this representation is commonly used by the compiler’s front-end, it can be also used as an IR. Small simplifications are allowed in this representation. We can find that Triton uses a tree to represent the different expressions executed by its symbolic execution engine, and it is used for different translations like: expression tree to Z3 for expressions solving, or expression tree to LLVM IR. Being honest, in my first design I included some structures in the IR to allow a tree design, but I wasn’t completely sure about it, so I removed it from the design.
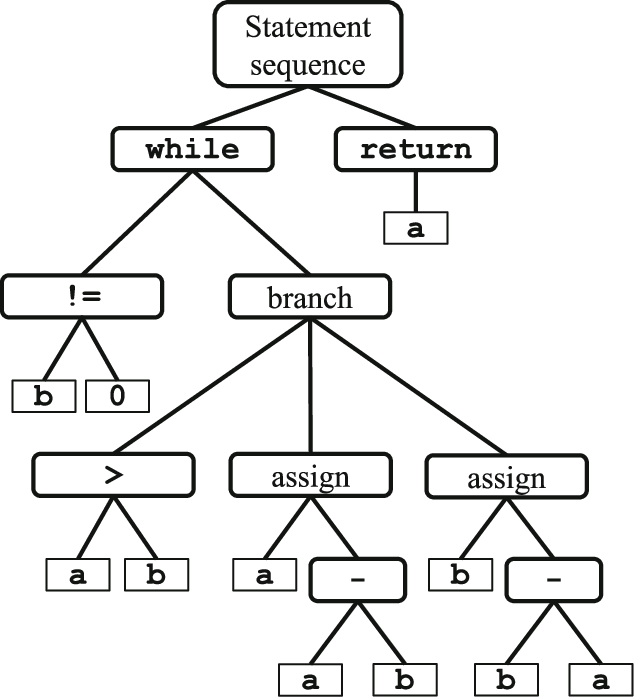

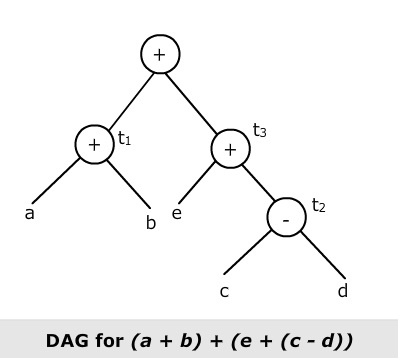
- Directed Acyclic Graph (DAG): this is one step simplified from the AST, in a compiler this DAG can provide us with the type and value of each node, but in binary analysis, this information should be recovered. Probably it could be more useful for a compiler than for a binary analysis tool, since the information that would be needed to be recovered for using it would require a big effort.
- Control-Flow Graph (CFG): this is a commonly used representation in binary analysis. A CFG is a graph in which blocks and edges represent the code and the control-flow of a function, in source code we can have that each block represents one statement from the source code, but in binary analysis commonly a block is a list of instructions (assembly or another intermediate language) with one entry point, and one exit point (a termination instruction, or an instruction to transfer the control of execution)

- Static-Single Assignment (SSA): this representation form represents an intermediate language with one restriction, the variables can be assigned only once, so their value cannot change. In case we want to give a new value to a previously defined variable, we create a new variable but with another subindex. This makes algorithms like def-use trivial (we’ll see later in a part dedicated to the implemented algorithms). In some cases, we will need a special instruction called phi to create a new value that will hold a value depending on where the control-flow came from.
- Linear IR: an intermediate representation that represents the instructions one after another as a sequence, which is similar to the assembly language. We have instructions to transfer values between memory and multiple registers etc. An example could be Dalvik’s bytecode, which is based on registers, and it is a kind of linear IR.
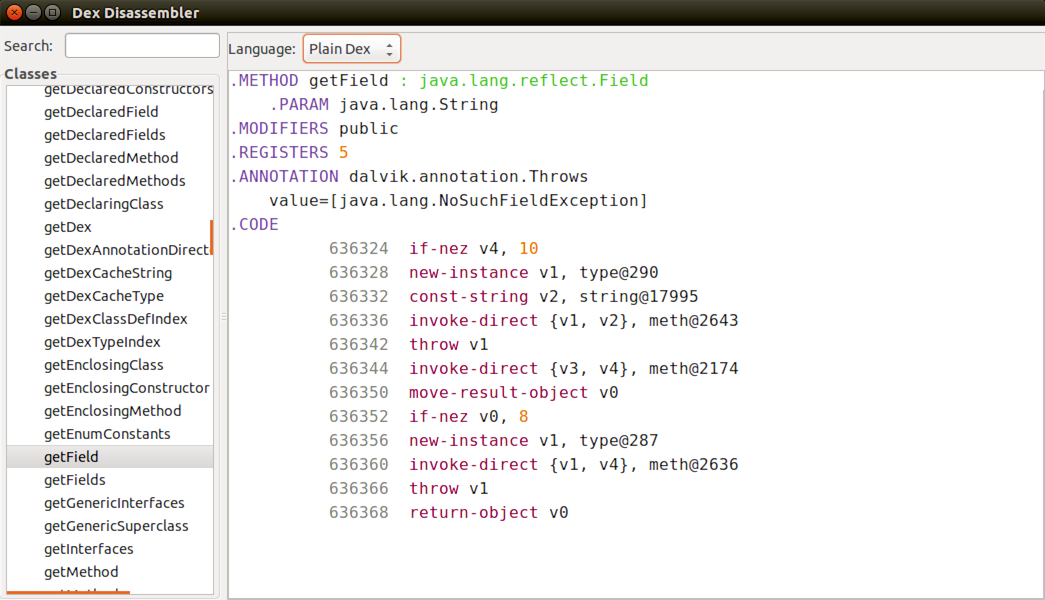
- Stack-Machine IR: In this case, we have a stack that is used to “store” values from the program, this kind of IR is designed to execute on a virtual stack machine. A good example of this one would be the bytecode of Java, which is stack-based.

In general, my observation from the different books and projects is that an IR has a container for storing functions/methods from the programs. As I said, many of the IRs I have used so far use a Control-Flow Graph representation, so inside this container we have a block structure, and inside of the blocks a list of instructions.
The blocks in the CFG will have a single point of entry, and a single point of exit. The point of exit can be an instruction that represents a jump, a conditional jump or a switch statement. We can also find some instructions that have only a fallthrough (another instruction that doesn’t jump). Or in another case, we can find an exit block that ends with a return or throwing an exception.
Finally, we have the instructions inside the blocks. These instructions can represent a subset of real assembly instructions, and they can be used to represent all the semantics from a real machine. Of course, the complexity of these IR instructions will depend on the machines we want to represent. Mostly, we should have the following category of instructions:
- Control-Flow instructions: instructions representing jumps, returns, switch, etc.
- Data-Flow instructions: instructions to access memory for reading or writing to memory.
- Operations: it wouldn’t be useful having access to memory data if we cannot work with that data, so here we have this category. The category would include binary operations, unary operations, comparisons, and assignments.
- Values: we need some type of data to work with. Memory can have different representations, for example, a map of addresses. We can have registers, these registers can represent those from the machine, or we could have virtual registers. In an SSA representation, we have an infinite number of registers, and each register can be assigned a value only once. Register and memory can have an associated type, or at least an associated size.
In the next section, we will cover all these different instructions from the point of view of MjolnIR, and what are the instructions that I decided to implement with a schematic view of the instructions. Later I will present the implementation in C++ code of the types and some of the design decisions.
MjolnIR - Structure of MjolnIR
Although I had many examples, deciding how to create one IR is not something very straightforward or easy, so my best resource in this case was reading about Binary Ninja ILs, and also the book Advanced Compiler Design & Implementation, in both resources they talk about three-levels of representation, from a more low level syntax like assembly to higher level closer to source code (llil-mlil-hlil), and I thought that the Medium Level IL was a good design for what I wanted to do.
First of all, I thought I would need to represent a Method from Dalvik, and the best way to represent a method was using a control-flow graph, and this control-flow graph would have blocks.
Secondly, the blocks would have instructions, but we have different types of instructions, so let’s call all of them statements, and here we have condition-flow instructions, a nop instruction, and return instructions. But a fundamental one was the expressions, these expressions are the instructions that perform operations, we have assignments, we have arithmetic-logic instructions, comparisons, call to instructions, and memory usage. These expressions are applied over registers which have a type, so we also have types representing different things like registers, memory, constant ints, called methods, classes and even temporal registers.
I joined all of these, and I ended up having a type of tree structure, I represented that structure using a (probably not really well) Backus-Naur form (BNF). In the next section, I will show the BNFs that represent all the statements from the IR, I will also talk about the different instructions that are part of that BNF and what I represent with them.
Backus-Naur forms
IRStmnt
At the top of the IR we have the statements, these will be every instruction from the IR that could be executed by the program, between these IRStmnt are the expressions (explained later), but more specific statements are those that change the Control-Flow Graph from the function/method, these are conditional and unconditional jumps, return statements, etc.
IRStmnt --> IRUJmp |
IRCJmp |
IRRet |
IRBlock |
IRNop |
IRSwitch |
IRExpr
IRUJmp --> jmp addr
IRCJmp --> if (IRStmnt) { jmp addr } NEXT fallthrough_addr
IRRet --> Ret IRStmnt
IRBlock --> IRStmnt1, IRStmnt2, ..., IRStmntN
IRSwitch --> switch (IRStmnt) { case X1 -> addr, case X2 -> addr, case XN -> addr }
All the instructions that are in a block are statements. Even the Blocks are statements. As I previously said, an IR needs Control-Flow instructions, these kinds of instructions would be:
- Unconditional jumps that specify the address where they jump.
- Conditional jumps that takes a comparison a statement and the address where to jump to in the case where the condition is met.
- Return instruction that can specify a returned value.
- Blocks, in my design blocks are statements too, and they contain a list of instructions.
- Switch, like conditional jumps but these take an expression for the value to check and lookup various cases of addresses where to jump to.
- Expressions, expressions are a special type of statements that will be subdivided into other instructions, we will see it in the next section.
IRExpr
The IR requires to support various instructions from the code, these are what we call IRExpr, these kinds of instructions don’t modify the control flow of the method but apply different kinds of operations to the variables/registers/memory in the program. They can affect the call-graph of a program, since one of the expressions allows calling other methods.
IRExpr --> IRBinOp |
IRUnaryOp |
IRAssign |
IRPhi |
IRCall |
IRLoad |
IRStore |
IRZComp |
IRBComp |
IRNew |
IRAlloca |
IRType
IRBinOp --> IRExpr <- IRExpr bin_op_t IRExpr
IRUnaryOp --> IRExpr <- unary_op_t IRExpr
IRAssign --> IRExpr <- IRExpr
IRPhi --> IRExpr <- IRExpr, IRExpr, ..., IRExpr
IRCall --> IRExpr(IRExpr1, IRExpr2, ..., IRExprN)
IRLoad --> IRExpr <- *IRExpr
IRStore --> *IRExpr <- IRExpr
IRZComp --> IRExpr zero_comp_t
IRBComp --> IRExpr comp_t IRExpr
IRNew --> IRExpr <- new IRExpr
IRAlloca --> IRExpr <- new IRExpr[IRExpr]
# kind of operations
bin_op_t --> ADD_OP_T |
SUB_OP_T |
S_MUL_OP_T |
U_MUL_OP_T |
S_DIV_OP_T |
U_DIV_OP_T |
MOD_OP_T
unary_op_t --> INC_OP_T |
DEC_OP_T |
NOT_OP_T |
NEG_OP_T |
CAST_OP_T |
Z_EXT_OP_T |
S_EXT_OP_T
zero_comp_t --> EQUAL_ZERO_T |
NOT_EQUAL_ZERO_T
comp_t --> EQUAL_T |
NOT_EQUAL_T |
GREATER_T |
GREATER_EQUAL_T |
LOWER_T |
ABOVE_T |
ABOVE_EQUAL_T |
BELOW_T
Here we have the second type of instructions, we have operations that work with data, loading and storing data in memory, assigning values to registers, doing comparisons and memory allocations, etc.
- Binary operations: those expressions that have two operands and store the result in a register/temporal register. We have different binary operations: add operation, sub operation, signed and unsigned multiplication and division, and finally mod operation.
- Unary operations: expressions that only use one operand, the result is stored in a register/temporal register. We have different unary operations: increment, decrement, not, neg, casting to a different type, zero extension and sign extension.
- Assignment operation: assign a value from one register/temporal register to another.
- PHI instruction: this instruction is used in IRs to represent the same value coming from different blocks. The Phi instruction has as many operands as predecessor blocks. Conceptually, Phi returns a value depending on which block is executed before the phi instruction.
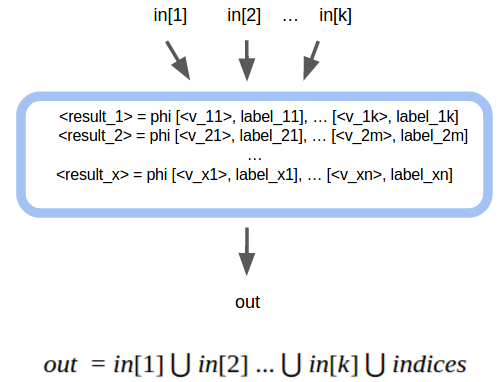
- Call instruction: this instruction has a Callee that is called, it gets a variable number of operands, and it optionally returns a value.
- Load and Store operations: used to load and store values from memory. In the case of Android, here we would have access to the class fields.
- Zero comparison operation: a comparison with a zero value, to know if the provided expression is equals or not equal to zero. The value returned by the operation is commonly used in a conditional jump.
- Binary comparison operation: this operation receives two expressions and a type of comparison, the available comparisons are equal, not equal, greater, greater-equal, lower, above, above-equal and below (for signed and unsigned comparisons). The value returned by the operation is commonly used in a conditional jump.
- New operation: used to initialize a new object.
- Alloca operation: used to initialize arrays with a specific size.
- Type: this is an especial expression that represents the different types available for the IR.
IRType
For supporting the types we find in the binary code, we have written a series of classes which derive from a superclass named IRType, as derived classes we have: registers, constant values, strings, memory, callee types.
IRType --> IRReg |
IRTempReg |
IRConstInt |
IRMemory |
IRString |
IRCallee |
IRField |
IRClass |
IRFundamental |
NONE
IRFundamental --> F_BOOLEAN |
F_BYTE |
F_CHAR |
F_DOUBLE |
F_FLOAT |
F_INT |
F_LONG |
F_SHORT |
F_VOID
Finally, we have values that are used in the expressions and also in the statements. Some IRs call some of these Values, others have registers, etc. In case of MjolnIR, I included registers that represent the registers from Dalvik, and also temporal registers that are used as results for some of the expression operations. Now we will list all of them with a description:
- Registers: used to represent the registers from Dalvik.
- Temporal registers: used as an intermediate storage for operations in the expressions.
- Constant Integers: integer values used, for example, in binary operations or comparisons.
- Memory: addresses of memory, including an accessed offset.
- String: a constant string value.
- Callee: a method called by the call instruction from the expressions.
- Field: a field from a Java-like language, the field contains information like the class it belongs, the name of the field, the type, etc.
- Class: a Java-like language class, with the name of the class.
- Fundamental: it represents the fundamental values available in a Java-like language.
Summary of the IR instructions
Next I show a summary of the IR:
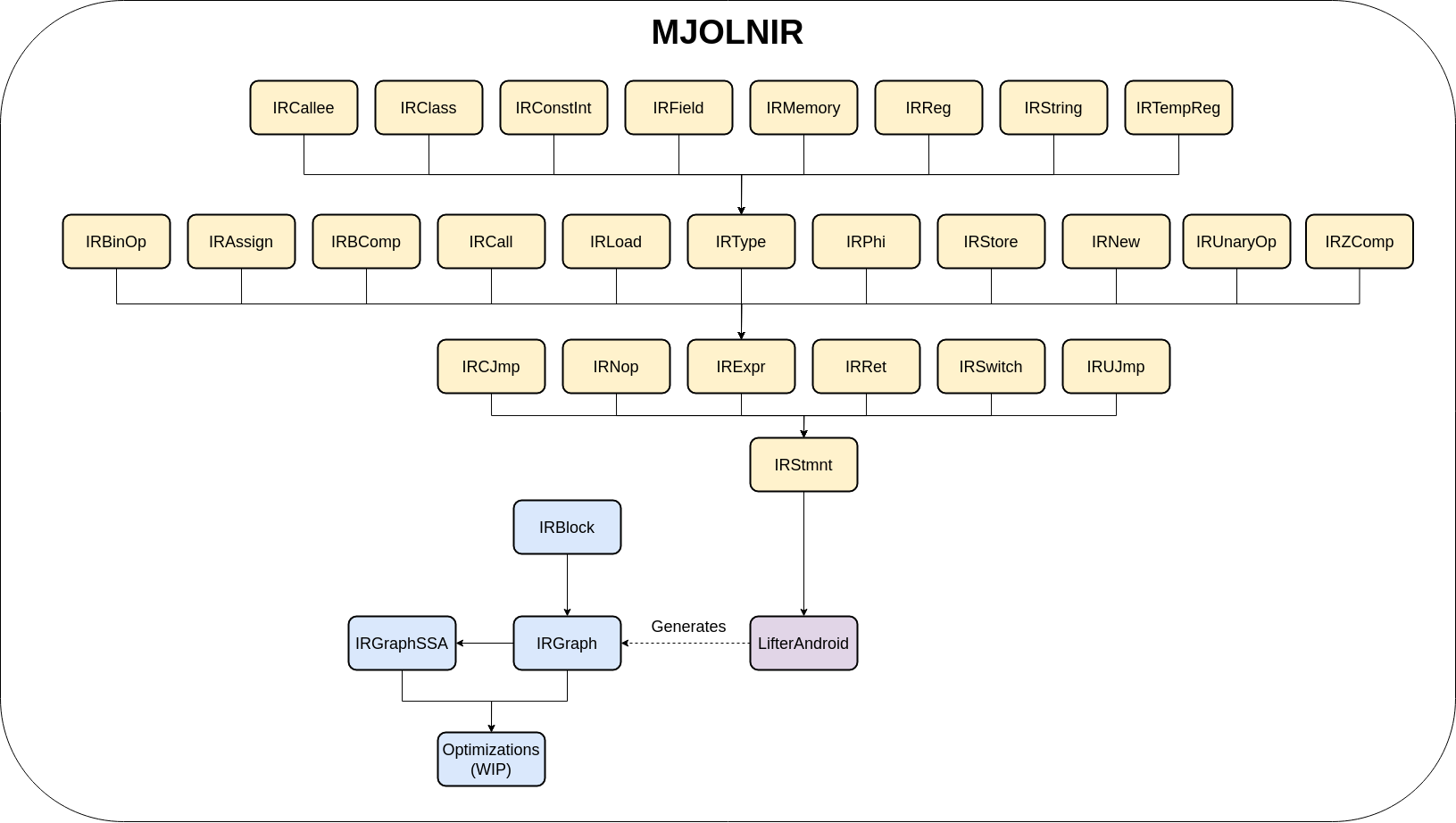
In this image, I include all the statements from the IR, together with that in the bottom of the image we have what will be later explained, the lifter from Dalvik to MjolnIR. The lifter generate IRGraphs that contains IRBlocks which contain a list of IRStmnts. Finally, from an IRGraph, an SSA form can be obtained, I will explain the algorithm used later. As part of the original idea, an optimizer was going to be written.
Implementation
The idea behind this post is not only providing a theoretical view like you can see in a compiler’s book, but also to provide a real life implementation of such an IR, and an explanation of it’s implementation. After explaining each one of the instructions, I will explain the different algorithms used for manipulating the CFG.
One clarification before starting, from now on I will use the following notation, I write the name of the classes using uppercase for the first character of the name, and in case of the IR all the classes start with IR followed by the name of the component that it represents (for example IRStmnt). Most of these classes have their version as a smart pointer, the name of the smart pointer type is the same as its class but in lowercase and followed by _t (for example IRBlock -> irblock_t). For the name of the variables and the name of the functions, I use snake case.
IRGraph Implementation
Although previously I wrote the BNF from IRGraph, here I will explain the implementation from the class.
First of all, for the graph we will change the notation and instead of having blocks or a pair of blocks, we will have nodes and edges. In C++ we will do this with using to give another name to the data types:
using Nodes = std::vector<irblock_t>;
using Edge = std::pair<irblock_t, irblock_t>;
using Edges = std::vector<Edge>;
using Paths = std::vector<std::vector<irblock_t>>;
Here we can see that the nodes are a vector of blocks, and the edges are a pair of blocks, and edges just a vector of edge. Finally, for some algorithms we will use Paths, which are a list of blocks.
Now we can move to see the implementation of a graph. I will not paste the implementation of the functions as I will explain some implementations later in depth, and also the whole code will be included in a repository with all the code.
class IRGraph {
IRGraph();
~IRGraph() = default;
bool add_node(irblock_t node);
void add_edge(irblock_t src, irblock_t dst);
void add_uniq_edge(irblock_t src, irblock_t dst);
void add_block_to_sucessors(irblock_t node, irblock_t successor);
void add_block_to_predecessors(irblock_t node, irblock_t predecessor);
Nodes& get_nodes();
Edges& get_edges();
std::optional<irblock_t> get_node_by_start_idx(std::uint64_t idx);
void merge_graph(irgraph_t graph);
void del_edge(irblock_t src, irblock_t dst);
void del_node(irblock_t node);
void delete_block_from_sucessors(irblock_t node, irblock_t block);
void delete_block_from_precessors(irblock_t node, irblock_t block);
std::vector<irblock_t> get_leaves();
std::vector<irblock_t> get_heads();
Paths find_path(irblock_t src,
irblock_t dst,
size_t cycles_count,
std::map<irblock_t, size_t> done);
Paths find_path_from_src(irblock_t src,
irblock_t dst,
size_t cycles_count,
std::map<irblock_t, size_t> done);
Nodes reachable_sons(irblock_t head);
Nodes reachable_parents(irblock_t leaf);
std::map<irblock_t, Nodes> compute_dominators(irblock_t head);
std::map<irblock_t, Nodes> compute_postdominators(irblock_t leaf);
std::map<irblock_t, irblock_t> compute_immediate_dominators();
std::map<irblock_t, irblock_t> compute_immediate_postdominators();
std::map<irblock_t, std::set<irblock_t>> compute_dominance_frontier();
irgraph_t copy();
// node information
size_t get_number_of_successors(irblock_t node);
Nodes& get_successors(irblock_t node);
size_t get_number_of_predecessors(irblock_t node);
Nodes& get_predecessors(irblock_t node);
node_type_t get_type_of_node(irblock_t node);
// algorithms from Advanced Compiler Design and Implementation
Nodes reachable_nodes_forward(irblock_t head);
Nodes reachable_nodes_backward(irblock_t leaf);
Nodes build_ebb(irblock_t r);
Nodes Depth_First_Search(irblock_t head);
Nodes Breadth_First_Search(irblock_t head);
void generate_dot_file(std::string name);
void generate_dominator_tree(std::string name);
const std::uint64_t get_cyclomatic_complexity();
void set_last_temporal(std::uint64_t last_temporal);
std::uint64_t get_last_temporal();
private:
Nodes nodes;
Edges edges;
std::map<irblock_t, Nodes> successors;
std::map<irblock_t, Nodes> predecessors;
std::uint64_t cyclomatic_complexity = -1;
std::uint64_t last_temporal;
}
As we can see, the graph contains the nodes which are a list of blocks, and the edges which are pairs of nodes (blocks connected through the control-flow). For each node, we store a list of successors and predecessors. And finally, some auxiliary variables, like the cyclomatic complexity of that function, and a variable that stores the last assigned temporal register.
For the graph, we have common utilities for adding blocks, removing them, connecting those blocks through edges, etc. But also other utilities not so common like: get_leaves to get nodes without successors, get_heads to get nodes without predecessors, find_path to find a connection between two blocks in the graph searching backwards, find_path_from_src to find a connection between two blocks in the graph searching forward, reachable_* that is used to get sons or parents, and others that implement common algorithms in graphs. For the last algorithms, I will explain them in-depth discussing the implementation code and the algorithm used.
IRBlock implementation
Now we can see the code from the basic blocks:
class IRBlock {
IRBlock();
~IRBlock() = default;
void add_statement_at_beginning(irstmnt_t statement);
void append_statement_to_block(irstmnt_t statement);
bool delete_statement_by_position(size_t pos);
size_t get_number_of_statements();
std::vector<irstmnt_t> &get_statements();
void set_start_idx(uint64_t start_idx);
void set_end_idx(uint64_t end_idx);
uint64_t get_start_idx();
uint64_t get_end_idx();
std::string get_name();
std::string to_string();
void set_phi_node();
void clear_phi_node();
bool contains_phi_node()
private:
bool phi_node = false;
//! starting idx and last idx (used for jump calculation)
uint64_t start_idx, end_idx;
//! statements from the basic block.
std::vector<irstmnt_t> block_statements;
}
The basic blocks do not contain much code, they just keep the first and the last index of their instructions, and information to know if a phi instruction exists in the block (for an explanation about the Phi instructions you can go to BNF section). Finally, the block contains a list of instructions belonging to that block. The included functions are just utilities for inserting instructions, deleting instructions, etc.
IRStmnt implementation
Now, we can see the implementation of the statements, as I previously said, the statements are the root of all the instructions (including the basic blocks). The statement class store also the enum with the type of the statements:
enum stmnt_type_t
{
UJMP_STMNT_T,
CJMP_STMNT_T,
RET_STMNT_T,
NOP_STMNT_T,
SWITCH_STMNT_T,
EXPR_STMNT_T,
NONE_STMNT_T = 99 // used to finish the chain of statements
};
Also, we have an enum for all the operations, I included this enum as part of IRStmnt class too, so we can check which operation we are working with if we have an IRStmnt.
enum op_type_t
{
UJMP_OP_T,
CJMP_OP_T,
RET_OP_T,
NOP_OP_T,
SWITCH_OP_T,
EXPR_OP_T,
BINOP_OP_T,
UNARYOP_OP_T,
ASSIGN_OP_T,
PHI_OP_T,
CALL_OP_T,
OP_T_OP_T,
LOAD_OP_T,
STORE_OP_T,
ZCOMP_OP_T,
BCOMP_OP_T,
NEW_OP_T,
ALLOCA_OP_T,
TYPE_OP_T,
REGISTER_OP_T,
TEMP_REGISTER_OP_T,
CONST_INT_OP_T,
CONST_FLOAT_OP_T,
FIELD_OP_T,
MEM_OP_T,
STRING_OP_T,
CLASS_OP_T,
CALLEE_OP_T,
FUNDAMENTAL_OP_T,
NONE_OP_T = 99 // used to finish the chain of statements
};
Having IRStmnt as the top of the classes allows to provide it as a value for many parameters, or for variables, then we can cast the pointers in order to work with different classes. Maybe using classes and inheritance is not the best way to generate the IR instructions, but it was the one I had in mind when I thought about providing statements as part of the other instructions.
Now we will see the IRStmnt class:
class IRStmnt
{
public:
IRStmnt(stmnt_type_t stmnt_type, op_type_t op_type);
virtual ~IRStmnt() = default;
stmnt_type_t get_statement_type();
op_type_t get_op_type();
std::string to_string();
const std::vector<irstmnt_t> &get_use_def_chain() const;
const std::unordered_map<irexpr_t, std::vector<irstmnt_t>> &get_def_use_chains() const;
std::optional<std::vector<irstmnt_t> *> get_def_use_chain_by_value(irexpr_t value);
void add_instr_to_use_def_chain(irstmnt_t instr);
void add_instr_to_def_use_chain(irexpr_t var, irstmnt_t instr);
void invalidate_chains();
void invalidate_use_def_chain();
void invalidate_def_use_chains();
void print_use_def_and_def_use_chain();
private:
//! Type of the statement.
stmnt_type_t stmnt_type;
//! Op type
op_type_t op_type;
//! Vectors used for use-def and def-use chains
std::vector<irstmnt_t> use_def_chain;
std::unordered_map<irexpr_t, std::vector<irstmnt_t>> def_use_chains;
};
This code represents the base of all the other instructions. As we can see, we have a couple of getters to know what kind the statement is, or what kind of operation it is. And then one of the most important parts. MjolnIR implemented both def-use and use-def chains, these are two lists that for each variable (register), it provides where the register is defined, and where it is used. Later I will provide a better description and the implementation of these algorithms. We have getters, setters and also functions to invalidate those chains.
IRUJmp implementation
Let’s see the implementation of an unconditional jump:
class IRUJmp : public IRStmnt
{
public:
IRUJmp(uint64_t addr, irblock_t target);
~IRUJmp() = default;
void set_jump_target(irblock_t target);
irblock_t get_jump_target();
uint64_t get_jump_addr();
std::string to_string();
private:
//! offset or address of target
uint64_t addr;
//! target where the jump will fall
irblock_t target;
};
The most important part of this instruction in the way I implemented it is the target. With this target, given a basic block, we can know where the block will jump.
IRCJmp implementation
Implementation of the conditional jump:
class IRCJmp : public IRStmnt
{
public:
IRCJmp(uint64_t addr, irstmnt_t condition, irblock_t target, irblock_t fallthrough);
~IRCJmp() = default;
uint64_t get_addr();
irstmnt_t get_condition();
void set_jump_target(irblock_t target);
irblock_t get_jump_target();
void set_fallthrough_Target(irblock_t fallthrough);
irblock_t get_fallthrough_target();
std::string to_string();;
private:
//! offset or address of target
uint64_t addr;
//! Condition for taking the target jump
irstmnt_t condition;
//! target where the jump will fall
irblock_t target;
//! fallthrough target.
irblock_t fallthrough;
};
The implementation is similar to IRUJmp, but in this case we need two targets, one taken if the condition matches, and another for the fallthrough target. The condition is provided as an IRStmnt so any expression or type can be given as a condition (probably in a better implementation, that condition should be restricted to a few types or expressions).
IRRet implementation
class IRRet : public IRStmnt
{
public:
IRRet(irstmnt_t ret_value);
~IRRet() = default;
irstmnt_t get_return_value();
std::string to_string();
private:
//! Returned value, commonly a NONE IRType, or an IRReg.
irstmnt_t ret_value;
};
A return instruction can optionally have a return value. A return instruction creates a leaf node, these are nodes that terminate the graph.
IRNop implementation
The nop instruction doesn’t receive any parameter, and can be used to create empty blocks (blocks that do nothing). So its implementation is pretty simple:
class IRRet : public IRStmnt
{
public:
IRRet(irstmnt_t ret_value);
~IRRet() = default;
irstmnt_t get_return_value();
std::string to_string();
private:
//! Returned value, commonly a NONE IRType, or an IRReg.
irstmnt_t ret_value;
};
IRSwitch implementation
The last type of jump is the switch instruction; switch allows given an expression, jumps to different blocks.
class IRSwitch : public IRStmnt
{
public:
IRSwitch(std::vector<int32_t> offsets,
irexpr_t condition,
std::vector<int32_t> constants_checks);
~IRSwitch() = default;
const std::vector<int32_t> &get_offsets() const;
irexpr_t get_condition();
const std::vector<int32_t> &get_constants_checks() const;
std::string to_string();
private:
//! switch offsets where instruction will jump.
std::vector<int32_t> offsets;
//! condition taken to decide where to jump
irexpr_t condition;
//! conditions checked during switch.
std::vector<int32_t> constants_checks;
};
We have a list of offsets and a list of checks for the case blocks from the switch statement. For the condition value, we have an expression (commonly a temporal register).
IRExpr implementation
Although the IRExpr instruction does not have itself a long codebase, it is the base class for all the expressions in MjolnIR, and it contains an enum to specify the type of expression we are working with:
enum expr_type_t
{
BINOP_EXPR_T,
UNARYOP_EXPR_T,
ASSIGN_EXPR_T,
PHI_EXPR_T,
CALL_EXPR_T,
TYPE_EXPR_T,
LOAD_EXPR_T,
STORE_EXPR_T,
ZCOMP_EXPR_T,
BCOMP_EXPR_T,
NEW_EXPR_T,
ALLOCA_EXPR_T,
NONE_EXPR_T = 99 // used to finish the expressions
};
Finally, the code from the IRExpr class, contains the code that other expressions will need to create:
class IRExpr : public IRStmnt
{
public:
IRExpr(expr_type_t type, op_type_t op_type);
~IRExpr() = default;
expr_type_t get_expression_type();
std::string to_string();
bool equals(irexpr_t irexpr);
friend bool operator==(IRExpr &, IRExpr &);
private:
//! ir expression as string
std::string ir_expr_str;
//! expression type
expr_type_t type;
};
IRBinOp implementation
One of the most important operations are binary operations, we have different mathematical operations we do with two operators, and then we store the result in another expression (commonly a register or a temporal register). This class is also the enum of the binary operations:
enum bin_op_t
{
// common arithmetic instructions
ADD_OP_T,
SUB_OP_T,
S_MUL_OP_T,
U_MUL_OP_T,
S_DIV_OP_T,
U_DIV_OP_T,
MOD_OP_T,
// common logic instructions
AND_OP_T,
XOR_OP_T,
OR_OP_T,
SHL_OP_T,
SHR_OP_T,
USHR_OP_T,
};
The implementation includes the two operands as expressions, and finally another expression as the place where to store the result
class IRBinOp : public IRExpr
{
public:
IRBinOp(bin_op_t bin_op_type,
irexpr_t result,
irexpr_t op1,
irexpr_t op2);
~IRBinOp() = default;
bin_op_t get_bin_op_type();
irexpr_t get_result();
irexpr_t get_op1();
irexpr_t get_op2();
std::string to_string();
bool equals(irbinop_t irbinop);
friend bool operator==(IRBinOp &, IRBinOp &);
private:
//! type of binary operation
bin_op_t bin_op_type;
//! IRBinOp => IRExpr(result) = IRExpr(op1) <binop> IRExpr(op2)
//! for the result we will have an IRExpr too.
irexpr_t result;
//! now each one of the operators
irexpr_t op1;
irexpr_t op2;
};
IRUnaryOp implementation
Similar as the previous operation, we have types of unary operations:
enum unary_op_t
{
NONE_UNARY_OP_T,
INC_OP_T,
DEC_OP_T,
NOT_OP_T,
NEG_OP_T,
CAST_OP_T, // maybe not used in binary
Z_EXT_OP_T, // zero extend
S_EXT_OP_T // sign extend
};
And because we have a cast operation, we have different casting operation enum values:
enum cast_type_t
{
NONE_CAST,
TO_BYTE,
TO_CHAR,
TO_SHORT,
TO_INT,
TO_LONG,
TO_FLOAT,
TO_DOUBLE,
TO_ADDR,
TO_BOOLEAN,
TO_CLASS,
TO_VOID,
TO_ARRAY,
};
As part of the implementation, we have a normal constructor that is used to initialize the unary operations, and in case of cast operation, we have another constructor that also initializes the type of cast operation. Also, if the cast is to a class, we can specify the name of the class we are casting too:
class IRUnaryOp : public IRExpr
{
public:
IRUnaryOp(unary_op_t unary_op_type,
irexpr_t result,
irexpr_t op);
/**
* @param cast_type: instruction is cast, specify type of cast.
*/
IRUnaryOp(unary_op_t unary_op_type,
cast_type_t cast_type,
irexpr_t result,
irexpr_t op);
/**
* @param cast_type: instruction is cast, specify type of cast.
* @param class_name: if cast is TO_CLASS, specify the name of the class.
*/
IRUnaryOp(unary_op_t unary_op_type,
cast_type_t cast_type,
std::string class_name,
irexpr_t result,
irexpr_t op);
~IRUnaryOp() = default;
unary_op_t get_unary_op_type();
irexpr_t get_result();
irexpr_t get_op();
void set_cast_type(cast_type_t cast_type);
cast_type_t get_cast_type();
std::string get_class_cast();
std::string to_string();
bool equals(irunaryop_t irunaryop);
friend bool operator==(IRUnaryOp &, IRUnaryOp &);
private:
//! type of unary operation
unary_op_t unary_op_type;
//! used for casting operations
cast_type_t cast_type;
//! Class casted to
std::string class_name;
//! IRUnaryOp => IRExpr(result) = <unaryop> IRExpr(op)
//! an IRExpr for where the result is stored.
irexpr_t result;
// operator
irexpr_t op;
};
The operand and the result are two expressions (commonly are registers or temporal registers).
IRAssign implementation
The implementation of this operation is similar to the previous one, since we have only one operand and one result. But conceptually it is very different because this operation is mostly used to move values between registers (registers/temporal registers). So instead of operand and result, we have source and destination. This instruction shouldn’t be used to move from or to memory, since we already have load and store for that.
class IRAssign : public IRExpr
{
public:
IRAssign(irexpr_t destination,
irexpr_t source);
~IRAssign() = default;
irexpr_t get_destination();
irexpr_t get_source();
std::string to_string();
bool equals(irassign_t irassign);
friend bool operator==(IRAssign &, IRAssign &);
private:
//! destination where the value will be stored.
irexpr_t destination;
//! source expression from where the value is taken
irexpr_t source;
};
IRPhi implementation
This instruction is a special instruction in an IR. An IR does not execute the code, but it represents the code. We have cases where the same variable can come from different paths, and depending on the path where the variable comes, its value is one or another. An example with source code would be like so:
#include <iostream>
int absolute(int x) {
if (x < 0) {
return -x;
} else {
return x;
}
}
int main() {
int value = -42;
int absValue = absolute(value);
std::cout << "Absolute value of " << value << " is " << absValue << std::endl;
return 0;
}
A simplified version of the IR, generated from absolute and generated with LLVM, would be like so:
define i32 @absolute(i32 %x) #0 {
entry:
%cmp = icmp slt i32 %x, 0
br i1 %cmp, label %if.then, label %if.end
if.then: ; preds = %entry
%neg = sub nsw i32 0, %x
br label %if.end
if.end: ; preds = %if.then, %entry
%retval.0 = phi i32 [ %x, %entry ], [ %neg, %if.then ]
ret i32 %retval.0
}
We have a phi instruction that, depending on what the last executed incoming block was, the value of %retval.0 will be %x if the code came from %entry, or %neg if it came from %if.then.
My implementation includes a map, the map has as a key which identifies the block from where the variable comes from, and as value the expression with the variable (register/temporal register). Finally, we have another expression as result, which will be the final register which will contain the value that will be used from that block.
class IRPhi : public IRExpr
{
public:
IRPhi();
~IRPhi() = default;
std::unordered_map<uint32_t, irexpr_t> &get_params();
void add_param(irexpr_t param, uint32_t id);
irexpr_t get_result();
void add_result(irexpr_t result);
std::string to_string();
bool equals(irphi_t irphi);
friend bool operator==(IRPhi &, IRPhi &);
private:
irexpr_t result;
std::unordered_map<uint32_t, irexpr_t> params;
};
IRCall implementation
The instruction IRCall was designed as a call to different types of functions. I implemented internal calls which are calls to functions in the binary, external calls which would be calls to library functions, and finally syscalls. The previous values are enum values in the code:
enum call_type_t
{
INTERNAL_CALL_T, // call to internal component
EXTERNAL_CALL_T, // call to external library (example DLL, .so file, external component, etc)
SYSCALL_T, // a syscall type
NONE_CALL_T = 99, // Not specified
};
The instruction stores as an IRExpr a callee, later we will see a type IRCallee that implements these functions for Java-type languages. Then the instruction also contains a vector for the parameters and an optional return value.
class IRCall : public IRExpr
{
public:
IRCall(irexpr_t callee,
std::vector<irexpr_t> args);
IRCall(irexpr_t callee,
call_type_t call_type,
std::vector<irexpr_t> args);
~IRCall() = default;
irexpr_t get_callee();
const std::vector<irexpr_t> &get_args() const;
std::string to_string();
void set_ret_val(irexpr_t ret_val);
irexpr_t get_ret_val();
call_type_t get_call_type();
bool equals(ircall_t ircall);
friend bool operator==(IRCall &, IRCall &);
private:
//! Type of call
call_type_t call_type;
//! Type representing the function/method called
irexpr_t callee;
//! Vector with possible arguments
std::vector<irexpr_t> args;
//! Return value (if it's for example a register)
irexpr_t ret_val;
};
The return value is optional, since we can have void return values, and parameters can be an empty vector.
IRLoad & IRStore implementations
I will put together these instructions since they represent a same concept. These two instructions are used to operate with memory. In the IR I tried to follow the convention pcode, and I created these instructions to operate with memory, so instead of working with memory directly in the operations, memory values are loaded in registers or in temporal registers. After that, we can operate with those values. The operations contains a destination and a source value expressed as IRExpr but it also has a size value (the size of the loaded or stored value), and also an index in case the memory is accessed using some index.
class IRLoad : public IRExpr
{
public:
/**
* @brief Constructor of IRLoad class, this class represent a load from memory (using memory or using register).
* @param destination: register where the value will be stored.
* @param source: expression from where the memory will be retrieved.
* @param size: loaded size.
* @return void
*/
IRLoad(irexpr_t destination,
irexpr_t source,
std::uint32_t size);
/**
* @brief Constructor of IRLoad class, this class represent a load from memory (using memory or using register).
* @param destination: register where the value will be stored.
* @param source: expression from where the memory will be retrieved.
* @param index: index from the load if this is referenced with an index.
* @param size: loaded size.
* @return void
*/
IRLoad(irexpr_t destination,
irexpr_t source,
irexpr_t index,
std::uint32_t size);
~IRLoad() = default;
irexpr_t get_destination();
irexpr_t get_source();
irexpr_t get_index();
std::uint32_t get_size();
std::string to_string();
bool equals(irload_t irload);
friend bool operator==(IRLoad &, IRLoad &);
private:
//! Register where the memory pointed by a register will be loaded.
irexpr_t destination;
//! Expression from where memory is read.
irexpr_t source;
//! Index if this is referenced by for example a register.
irexpr_t index;
//! Size of loaded value
std::uint32_t size;
};
class IRStore : public IRExpr
{
public:
/**
* @brief Constructor of IRStore class, this represent an store to memory instruction.
* @param destination: Expression where value is written to.
* @param source: register with the value to be stored.
* @param size: size of the stored value.
* @return void
*/
IRStore(irexpr_t destination,
irexpr_t source,
std::uint32_t size);
/**
* @brief Constructor of IRStore class, this represent an store to memory instruction.
* @param destination: Expression where value is written to.
* @param source: register with the value to be stored.
* @param index: index where value is stored.
* @param size: size of the stored value.
* @return void
*/
IRStore(irexpr_t destination,
irexpr_t source,
irexpr_t index,
std::uint32_t size);
~IRStore() = default;
irexpr_t get_destination();
irexpr_t get_source();
irexpr_t get_index();
std::uint32_t get_size();
std::string to_string();
bool equals(irstore_t irstore);
friend bool operator==(IRStore &, IRStore &);
private:
//! Memory pointed by register where value will be stored.
irexpr_t destination;
//! Expression with source of value to be stored.
irexpr_t source;
//! Index if this is referenced by for example a register.
irexpr_t index;
//! Size of stored value
std::uint32_t size;
};
IRZComp implementation
Since this IR was mainly implemented for Java-like languages, I implemented an instruction to compare with a zero value. There are different enum values that will tell the type of comparator:
enum zero_comp_t
{
EQUAL_ZERO_T, // ==
NOT_EQUAL_ZERO_T, // !=
LOWER_ZERO_T, // <
GREATER_EQUAL_ZERO, // >=
GREATER_ZERO_T, // >
LOWER_EQUAL_ZERO // <=
};
Then the instruction contains a register for the compared operand, and a register for storing the result. In both cases the values are provided as IRExpr:
class IRZComp : public IRExpr
{
public:
/**
* @brief Constructor of IRZComp, this is a comparison with zero.
* @param comp: type of comparison (== or !=).
* @param result: register or temporal register where result is stored.
* @param reg: register used in the comparison.
* @return void
*/
IRZComp(zero_comp_t comp,
irexpr_t result,
irexpr_t reg);
~IRZComp() = default;
irexpr_t get_result();
irexpr_t get_reg();
zero_comp_t get_comparison();
std::string to_string();
bool equals(irzcomp_t irzcomp);
friend bool operator==(IRZComp &, IRZComp &);
private:
//! Register where result is stored
irexpr_t result;
//! Register for comparison with zero.
irexpr_t reg;
//! Type of comparison
zero_comp_t comp;
};
IRBComp implementation
In the case, we do not compare with zero, but between two registers, we use this instruction. Again we have different types of comparisons:
enum comp_t
{
EQUAL_T, // ==
NOT_EQUAL_T, // !=
GREATER_T, // >
GREATER_EQUAL_T, // >=
LOWER_T, // <
LOWER_EQUAL_T, // <=
ABOVE_T, // (unsigned) >
ABOVE_EQUAL_T, // (unsigned) >=
BELOW_T, // (unsigned) <
};
The instruction implementation is almost the same as the previous one, but this time with two registers as operators:
class IRBComp : public IRExpr
{
public:
/**
* @brief Constructor of IRBComp, this class represent a comparison between two types.
* @param comp: type of comparison from an enum.
* @param result: register or temporal register where result is stored.
* @param reg1: first type where the comparison is applied.
* @param reg2: second type where the comparison is applied.
* @return void
*/
IRBComp(comp_t comp,
irexpr_t result,
irexpr_t reg1,
irexpr_t reg2);
~IRBComp() = default;
irexpr_t get_result();
irexpr_t get_reg1();
irexpr_t get_reg2();
comp_t get_comparison();
std::string to_string();
bool equals(irbcomp_t bcomp);
friend bool operator==(IRBComp &, IRBComp &);
private:
//! register or temporal register where result is stored
irexpr_t result;
//! registers used in the comparisons.
irexpr_t reg1;
irexpr_t reg2;
//! Type of comparison
comp_t comp;
};
IRNew implementation
Java-type languages contain a new instruction for allocating memory for a new object. This instruction contains a result value (which will be a register) and a class instance that will be the type of the new object. We will later see in types the IRClass:
class IRNew : public IRExpr
{
public:
/**
* @brief Construct a new IRNew::IRNew object which represents
* the creation of an instance of a class.
*
* @param result: result register where object is stored.
* @param class_instance: IRClass object which represent the instance.
* @return void
*/
IRNew(irexpr_t result,
irexpr_t class_instance);
~IRNew() = default;
irexpr_t get_result();
irexpr_t get_source_class();
std::string to_string();
bool equals(irnew_t new_i);
friend bool operator==(IRNew &, IRNew &);
private:
//! register where the result will be stored.
irexpr_t result;
//! class type which will create a new instance.
irexpr_t class_instance;
};
IRAlloca implementation
In opposite to a new instruction, we can allocate memory to store an array. In Java-type languages, the arrays are allocated as objects. IRAlloca has this purpose, allocating memory for an array. And for that reason IRAlloca has a size value:
class IRAlloca : public IRExpr
{
public:
/**
* @brief Construct a new IRAlloca object, this kind of
* expression creates "allocates" memory for an array
* having this class will be useful also for allocating
* memory in other architectures.
*
* @param result register or address where data will be stored
* @param type_instance type to create an array
* @param size size of the given array
*/
IRAlloca(irexpr_t result,
irexpr_t type_instance,
irexpr_t size);
~IRAlloca() = default;
irexpr_t get_result()
irexpr_t get_source_type();
irexpr_t get_size();
std::string to_string();
bool equals(iralloca_t alloca);
friend bool operator==(IRAlloca &, IRAlloca &);
private:
//! register or variable where result will be stored.
irexpr_t result;
//! type which it will create a new instance
irexpr_t type_instance;
//! size of the allocated space
irexpr_t size;
};
IRType implementation
Finally, we arrive to the objects that represent the operands of the operations, the memory, the classes, the fields, etc. For that reason, IRType contains an enum that specify the type:
enum type_t
{
REGISTER_TYPE = 0,
TEMP_REGISTER_TYPE,
CONST_INT_TYPE,
CONST_FLOAT_TYPE,
FIELD_TYPE,
MEM_TYPE,
STRING_TYPE,
CLASS_TYPE,
CALLEE_TYPE,
FUNDAMENTAL_TYPE,
NONE_TYPE = 99
};
An idea I had was to store the order of the memory access. Commonly architectures like x86, x86-64 stores the memory in a format known as little-endian, but other architectures can store the data in big-endian, even the crazy idea of a middle-endian exists!!! You can read more about endianness at wikipedia:
enum mem_access_t
{
LE_ACCESS = 0, //! little-endian access
BE_ACCESS, //! big-endian access
ME_ACCESS, //! This shouldn't commonly happen?
NONE_ACCESS = 99
};
The instruction stores the type, a name to represent the type, even a field for annotations to store and show from the type.
class IRType : public IRExpr
{
public:
/**
* @brief Constructor of the IRType, this will be the generic type used for the others.
* @param type: type of the class.
* @param op_type: global type of operation
* @param type_name: name used for representing the type while printing.
* @param type_size: size of the type in bytes.
* @return void
*/
IRType(type_t type, op_type_t op_type, std::string type_name, size_t type_size);
~IRType() = default;
std::string get_type_name();
size_t get_type_size();
type_t get_type();
virtual std::string get_type_str();
mem_access_t get_access();
void write_annotations(std::string annotations);
std::string read_annotations();
std::string to_string();
bool equal(irtype_t type);
friend bool operator==(IRType &, IRType &);
private:
//! type value as a type_t
type_t type;
//! name used to represent the type in IR representation.
std::string type_name;
//! size of the type, this can vary depending on architecture
//! and so on.
size_t type_size;
//! annotations are there for you to write whatever you want
std::string annotations;
};
IRReg implementation
The IRs commonly operate with values or with registers. These are the basic types in the operations. The registers can be those from the architecture using the name of that computer architecture, or like in SSA-form IRs we can use an infinite set of registers. Compilers when they transform from IR to assembly apply different optimizations to reduce the number of registers, and then to assign the registers from the IR, to those from the real machine. In the case of virtual architectures like dalvik, the VM has 64K registers for each called method, since these are virtual registers. The registers of MjolnIR contain an id, and depending on the architecture, the id can represent one register from that architecture or not. Although I didn’t use it, following Triton’s implementation, I created the next types (but I didn’t ever use them…):
const int x86_arch = 1;
enum x86_regs_t
/**
* @brief X86 registers, enums for IR, sizes and strings.
*/
{
// General purpose registers
rax, eax, ax, ah, al,
rbx, ebx, bx, bh, bl,
rcx, ecx, cx, ch, cl,
rdx, edx, dx, dh, dl,
// pointer registers
rdi, edi, di,
rsi, esi, si,
// stack registers
rbp, ebp, bp,
rsp, esp, sp,
// program counter
rip, eip, ip,
// extended registers in x86-64
r8, r8d, r8w, r8b,
r9, r9d, r9w, r9b,
r10, r10d, r10w, r10b,
r11, r11d, r11w, r11b,
r12, r12d, r12w, r12b,
r13, r13d, r13w, r13b,
r14, r14d, r14w, r14b,
r15, r15d, r15w, r15b,
// flags for state representation
eflags,
mm0, mm1, mm2, mm3, mm4, mm5, mm6, mm7,
zmm0, zmm1, zmm2, zmm3, zmm4, zmm5, zmm6,
zmm7, zmm8, zmm9, zmm10, zmm11, zmm12, zmm13,
zmm14, zmm15, zmm16, zmm17, zmm18, zmm19, zmm20,
zmm21, zmm22, zmm23, zmm24, zmm25, zmm26, zmm27,
zmm28, zmm29, zmm30, zmm31, mxcsr,
cr0, cr1, cr2, cr3, cr4, cr5, cr6, cr7, cr8, cr9,
cr10, cr11, cr12, cr13, cr14, cr15,
cs, ds, es, fs, gs, ss,
dr0, dr1, dr2, dr3, dr6, dr7
};
static const std::unordered_map<x86_regs_t, size_t> x86_regs_size = {
{rax,8}, {eax,4}, {ax,2}, {ah,1}, {al,1},
{rbx,8}, {ebx,4}, {bx,2}, {bh,1}, {bl,1},
{rcx,8}, {ecx,4}, {cx,2}, {ch,1}, {cl,1},
{rdx,8}, {edx,4}, {dx,2}, {dh,1}, {dl,1},
{rdi,8}, {edi,4}, {di,2},
{rsi,8}, {esi,4}, {si,2},
{rip,8}, {eip,4}, {ip,2},
{r8, 8}, {r8d,4}, {r8w,2}, {r8b,1},
{r9, 8}, {r9d,4}, {r9w,2}, {r9b,1},
{r10, 8}, {r10d,4}, {r10w,2}, {r10b,1},
{r11, 8}, {r11d,4}, {r11w,2}, {r11b,1},
{r12, 8}, {r12d,4}, {r12w,2}, {r12b,1},
{r13, 8}, {r13d,4}, {r13w,2}, {r13b,1},
{r14, 8}, {r14d,4}, {r14w,2}, {r14b,1},
{r15, 8}, {r15d,4}, {r15w,2}, {r15b,1}
};
static const std::unordered_map<x86_regs_t, std::string> x86_regs_name = {
{rax,"rax"}, {eax,"eax"}, {ax,"ax"}, {ah,"ah"}, {al,"al"},
{rbx,"rbx"}, {ebx,"ebx"}, {bx,"bx"}, {bh,"bh"}, {bl,"bl"},
{rcx,"rcx"}, {ecx,"ecx"}, {cx,"cx"}, {ch,"ch"}, {cl,"cl"},
{rdx,"rdx"}, {edx,"edx"}, {dx,"dx"}, {dh,"dh"}, {dl,"dl"},
{rdi,"rdi"}, {edi,"edi"}, {di,"di"},
{rsi,"rsi"}, {esi,"esi"}, {si,"si"},
{rip,"rip"}, {eip,"eip"}, {ip,"ip"},
{r8,"r8"}, {r8d,"r8d"}, {r8w,"r8w"}, {r8b,"r8b"},
{r9,"r9"}, {r9d,"r9d"}, {r9w,"r9w"}, {r9b,"r9b"},
{r10,"r10"}, {r10d,"r10d"}, {r10w,"r10w"}, {r10b,"r10b"},
{r11,"r11"}, {r11d,"r11d"}, {r11w,"r11w"}, {r11b,"r11b"},
{r12,"r12"}, {r12d,"r12d"}, {r12w,"r12w"}, {r12b,"r12b"},
{r13,"r13"}, {r13d,"r13d"}, {r13w,"r13w"}, {r13b,"r13b"},
{r14,"r14"}, {r14d,"r14d"}, {r14w,"r14w"}, {r14b,"r14b"},
{r15,"r15"}, {r15d,"r15d"}, {r15w,"r15w"}, {r15b,"r15b"}
};
The first implementation of MjolnIR wasn’t using an SSA form but directly used the values from Dalvik. Later I implemented the SSA form, and for that the IRReg contains a sub_id field, to express the SSA form in the registers:
class IRReg : public IRType
{
public:
/**
* @brief Constructor of IRReg type.
* @param reg_id: id of the register this can be an enum if is a well known register, or just an id.
* @param current_arch: curreng architecture to create the register.
* @param type_name: string for representing the register.
* @param type_size: size of the register.
* @return void
*/
IRReg(std::uint32_t reg_id, int current_arch, std::string type_name, size_t type_size);
/**
* @brief Constructor of IRReg type.
* @param reg_id: id of the register this can be an enum if is a well known register, or just an id.
* @param reg_sub_id: sub id of the register used in the SSA form.
* @param current_arch: curreng architecture to create the register.
* @param type_name: string for representing the register.
* @param type_size: size of the register.
* @return void
*/
IRReg(std::uint32_t reg_id, std::int32_t reg_sub_id, int current_arch, std::string type_name, size_t type_size);
~IRReg() = default;
std::uint32_t get_id();
std::uint32_t get_sub_id();
int get_current_arch();
std::string get_type_str();
mem_access_t get_access();
std::string to_string();
bool same(irreg_t reg);
bool equal(irreg_t reg);
friend bool operator==(IRReg &, IRReg &);
private:
//! id of the register, this will be an enum
//! in case the arquitecture contains a known set
//! of registers, for example x86-64 will have a
//! well known set of registers, e.g. EAX, AX, RSP
//! RIP, etc.
//! Other arquitectures like DEX VM will not have
//! an specific set.
std::uint32_t id;
//! sub id of the register, this sub id will be used
//! in the SSA form, and used to check if a register
//! is the same than other.
std::int32_t sub_id;
int current_arch;
};
IRTempReg implementation
In some cases, the instructions implement intrinsic operands, an IR instead of representing instrinsic operands it can use registers. In MjolnIR for doing so, I implemented temporal registers. For example, if a language uses 3 operands like the next:
int x = 2;
int y = 1;
int z = 5;
int d = x + y + z;
Commonly an IR instruction only contains two operands, and then the result value. For that reason we can use a temporal register to represent the previous sequence of instructions in the next way:
int x = 2;
int y = 1;
int z = 5;
temp_reg1 = x + y;
int d = temp_reg1 + z;
Now the instruction only has two operands. For doing these operations, MjolnIR uses IRTempReg operands:
class IRTempReg : public IRType
{
public:
/**
* @brief Constructor of IRTempReg type.
* @param reg_id: id of the register this will be an incremental id.
* @param type_name: string for representing the register.
* @param type_size: size of the register.
* @return void
*/
IRTempReg(std::uint32_t reg_id, std::string type_name, size_t type_size);
~IRTempReg() = default;
std::uint32_t get_id();
std::string get_type_str();
mem_access_t get_access();
std::string to_string();
bool equal(irtempreg_t temp_reg);
friend bool operator==(IRTempReg &, IRTempReg &);
private:
//! This id will be just an incremental number
//! as these are temporal registers.
std::uint32_t id;
};
IRConstInt implementation
This object is just a wrapper for constant integer values. It is also used to store metadata like if the value is signed or not, and the byte order (this maybe was a foolish decision on my side…). Since a possible optimization for obfuscated values was constant folding, I implemented the different operators on the class. The operators internally check if the values are signed or unsigned, and finally return another IRConstInt with the proper size:
IRConstInt operator+(IRConstInt &a, IRConstInt &b)
{
if (a.is_signed)
{
int64_t result = static_cast<int64_t>(a.value) + static_cast<int64_t>(b.value);
IRConstInt res(result, a.is_signed, a.byte_order, a.get_type_name(), a.get_type_size());
return res;
}
uint64_t result = a.value + b.value;
IRConstInt res(result, a.is_signed, a.byte_order, a.get_type_name(), a.get_type_size());
return res;
}
Next, the implementation of IRConstInt:
class IRConstInt : public IRType
{
public:
/**
* @brief Constructor of IRConstInt this represent any integer used in the code.
* @param value: value of the constant integer
* @param is_signed: is signed value (true) or unsigned (false).
* @param byte_order: byte order of the value.
* @param type_name: name used for representing the value.
* @param type_size: size of the integer.
* @return void
*/
IRConstInt(std::uint64_t value, bool is_signed, mem_access_t byte_order, std::string type_name, size_t type_size);
~IRConstInt() = default;
bool get_is_signed();
std::string get_type_str();
mem_access_t get_access();
uint64_t get_value_unsigned();
int64_t get_value_signed();
std::string to_string();
bool equal(irconstint_t const_int);
friend bool operator==(IRConstInt &, IRConstInt &);
friend IRConstInt operator+(IRConstInt &a, IRConstInt &b);
friend IRConstInt operator-(IRConstInt &a, IRConstInt &b);
friend IRConstInt operator/(IRConstInt &a, IRConstInt &b);
friend IRConstInt operator*(IRConstInt &a, IRConstInt &b);
friend IRConstInt operator%(IRConstInt &a, IRConstInt &b);
friend IRConstInt operator&(IRConstInt &a, IRConstInt &b);
friend IRConstInt operator|(IRConstInt &a, IRConstInt &b);
friend IRConstInt operator^(IRConstInt &a, IRConstInt &b);
friend IRConstInt operator<<(IRConstInt &a, IRConstInt &b);
friend IRConstInt operator>>(IRConstInt &a, IRConstInt &b);
friend IRConstInt operator++(IRConstInt &a, int);
friend IRConstInt operator--(IRConstInt &a, int);
friend IRConstInt operator!(IRConstInt &a);
friend IRConstInt operator~(IRConstInt &a);
private:
//! Value of the integer
std::uint64_t value;
//! Check to know if the constant is a unsigned
//! or signed value.
bool is_signed;
//! byte order of the value.
mem_access_t byte_order;
};
IRMemory implementation
Memory operands are specified as the memory address, an offset, a byte order and a size.
class IRMemory : public IRType
{
public:
/**
* @brief IRMemory constructor this represent a memory address with accessed offset and size.
* @param mem_address: address of the memory.
* @param offset: offset accessed (commonly 0).
* @param byte_order: byte order of the memory (LE, BE, ME?).
* @param type_name: memory representation with a string.
* @param type_size: size of the memory.
* @return void
*/
IRMemory(std::uint64_t mem_address, std::int32_t offset, mem_access_t byte_order, std::string type_name, size_t type_size);
~IRMemory() = default;
std::uint64_t get_mem_address();
std::int32_t get_offset();
std::string get_type_str();
mem_access_t get_access();
std::string to_string();
bool equal(irmemory_t memory);
friend bool operator==(IRMemory &, IRMemory &);
private:
//! accessed address
std::uint64_t mem_address;
//! offset of the memory accessed
std::int32_t offset;
//! byte order of the memory.
mem_access_t byte_order;
};
IRString implementation
Languages like C or C++, represent strings as constant strings in read-only memory, and then a pointer is used to access that data. Java-type languages use String objects. This operand is used to represent those string constant values:
class IRString : public IRType
{
public:
/**
* @brief Constructor of IRString class, this represent strings used in code.
* @param str_value: value of that string.
* @param type_name: some meaninful string name.
* @param type_size: size of the type (probably here string length)
* @return void
*/
IRString(std::string str_value, std::string type_name, size_t type_size);
~IRString() = default;
std::string get_str_value();
std::string get_type_str();
mem_access_t get_access();
std::string to_string();
bool equal(irstring_t str);
friend bool operator==(IRString &, IRString &);
private:
//! string value, probably nothing more will be here
std::string str_value;
};
IRClass implementation
For instructions like IRNew a class is provided as parameter to specify the object type of the created object. IRClass just stores the fully qualified name of the class.
class IRClass : public IRType
{
public:
/**
* @brief Constructor of IRClass, this represent the name of a class
* that is assigned as a type.
* @param class_name: name of the class.
* @param type_name: should be the same value than previous one.
* @param type_size: should be 0.
* @return void
*/
IRClass(std::string class_name, std::string type_name, size_t type_size);
~IRClass() = default;
std::string get_class();
std::string get_type_str();
mem_access_t get_access();
std::string to_string();
bool equal(irclass_t class_);
friend bool operator==(IRClass &, IRClass &);
private:
//! class name including path, used for instructions
//! of type const-class
std::string class_name;
};
IRCallee implementation
In binaries created from languages like C or C++, a call specifies a register or an address where to jump, and if there are no symbols, an analysis must be done to obtain how many parameters are passed to the call. In Java-type languages, these called methods are specified by class, name and the description of the method. That description contains the return type and the parameters. MjolnIR was thought to support both, but I implemented for Dalvik, so I had all the method descriptions. IRCallee stores all that information:
class IRCallee : public IRType
{
public:
/**
* @brief Constructor of IRCallee this represent any function/method called by a caller!
* @param addr: address of the function/method called (if available).
* @param name: name of the function/method called (if available).
* @param class_name: name of the class from the method called (if available).
* @param n_of_params: number of the parameters for the function/method (if available).
* @param description: description of the parameters from the function/method (if available).
* @param type_name: some meaninful string name.
* @param type_size: size of the type (probably here 0)
* @return void
*/
IRCallee(std::uint64_t addr,
std::string name,
std::string class_name,
int n_of_params,
std::string description,
std::string type_name,
size_t type_size);
~IRCallee() = default;
std::uint64_t get_addr();
std::string get_name();
std::string get_class_name();
int get_number_of_params();
std::string get_description();
std::string get_type_str();
mem_access_t get_access();
std::string to_string();
bool equal(ircallee_t callee);
friend bool operator==(IRCallee &, IRCallee &);
private:
//! for those functions of binary formats we will mostly have the address
//! only, these can be from a library, from the same binary, etc.
std::uint64_t addr;
//! name of the callee function or method, this can be resolved from the
//! binary symbols if those exist or is given in case of other formats.
std::string name;
//! in case it is a method, probably we will need to know class name
//! for possible analysis which requires to know about a calls.
std::string class_name;
//! there are cases where functions/methods can have the same name but
//! different parameters, you can give the number of parameters (if recognized)
//! or the string with the description of the method
int n_of_params;
std::string description;
};
IRField implementation
Java-type languages are object-oriented programming languages, and we create classes, these classes can contain methods, but also they can store fields. Fields are variables global to the objects that can be used in any method. The field can have different types, and these are expressed as an enum value:
enum field_t
{
CLASS_F,
BOOLEAN_F,
BYTE_F,
CHAR_F,
DOUBLE_F,
FLOAT_F,
INT_F,
LONG_F,
SHORT_F,
VOID_F,
ARRAY_F
};
Then the fields in Mjolnir contain the name of the class, the name of the field, the type, and in case it is a class, the name of the class.
class IRField : public IRType
{
public:
/**
* @brief Construct a new IRField::IRField object
*
* @param class_name: class name of the field
* @param type: type from field_t
* @param field_name: name of the field.
* @param type_name: some meaninful string name.
* @param type_size: size of the type (probably here 0)
*/
IRField(std::string class_name,
field_t type,
std::string field_name,
std::string type_name,
size_t type_size);
IRField(std::string class_name,
std::string type_class_name,
std::string field_name,
std::string type_name,
size_t type_size);
~IRField() = default;
std::string get_class_name();
field_t get_type();
std::string get_type_class();
std::string get_name();
std::string to_string();
bool equal(irfield_t field);
friend bool operator==(IRField &, IRField &);
private:
//! Class name of the field
std::string class_name;
//! Type of the field
field_t type;
//! if type is class set class name
std::string type_class;
//! Field name
std::string field_name;
};
IRFundamental type
In the case where we want to do data analysis and assign a type to registers or temporal registers, we can use a fundamental value. Fundamental values are provided as an enum:
enum fundamental_t
{
F_BOOLEAN,
F_BYTE,
F_CHAR,
F_DOUBLE,
F_FLOAT,
F_INT,
F_LONG,
F_SHORT,
F_VOID
};
Finally, this fundamental object only contains this enum value.
class IRFundamental : public IRType
{
public:
IRFundamental(fundamental_t type, std::string type_name);
~IRFundamental() = default;
fundamental_t get_type();
std::string to_string();
private:
fundamental_t type;
};
MjolnIR - Graph Algorithms
In this part of the post, we’ll dig deeper into the graph algorithms I implemented into MjolnIR. Graph algorithms can be useful to detect possible behaviors in a control-flow graph, for example, to understand from which nodes the control-flow goes from the beginning of a method to a given node. We can also use them to go over a control-flow graph in depth or in breadth order. Most of the theory from this part will be directly extracted from the book Advanced Compiler Design by Steven S. Muchnick. This is a review of an implementation, so I think it’s okay to take the theory from a well-written book.
Dominators
Having a Control-Flow Graph, we can detect things like loops in that CFG. To do that, we need to define a relation called dominance between nodes. We have that a node d dominates a node i (d dom i), if every path from the entry node to the node i goes over d (ALWAYS!!!)
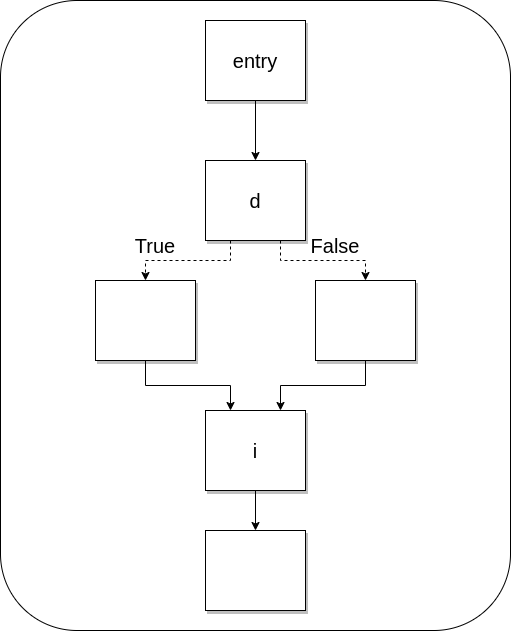
In the previous image we can clearly see that it doesn’t matter where control comes from to i, it always goes through d.
dom is a reflexive relation (every node dominates itself), transitive (if a dom b and b dom c, then a dom c), and also antisymmetric (if a dom b and b dom a clearly a=b). Later we will see another relation called immediate dominance. Next we can see the pseudo-code given by Muchnick:

Now, we will analyze the implementation used in MjolnIR. First of all, let’s see how the function was:
std::map<irblock_t, Nodes> compute_dominators(irblock_t head);
The function returns a map with all the blocks, and for each block, the value is the list of dominator nodes. As a parameter, the head from the CFG is given as a starting point to start calculating the dominators.
First of all, we will calculate all the reachable_sons of the head block provided by parameter, these reachable_sons are the nodes we can reach forward from the provided node:
std::map<irblock_t, Nodes> IRGraph::compute_dominators(irblock_t head)
{
std::map<irblock_t, Nodes> dominators;
auto nodes = reachable_sons(head);
The implementation of reachable_sons directly calls to reachable_nodes_forward, as I said, are all the nodes we can reach from the provided node, to calculate this, we will go through the successors of the head node, then from the successors we will go to their successors, and so on:
Nodes IRGraph::reachable_sons(irblock_t head)
{
return IRGraph::reachable_nodes_forward(head);
}
Nodes IRGraph::reachable_nodes_forward(irblock_t head)
{
Nodes todo;
Nodes reachable;
todo.push_back(head);
while (!todo.empty())
{
// similar to python pop.
auto node_it = todo.begin();
auto node = *node_it;
todo.erase(node_it);
// node already in reachable
if (std::find(reachable.begin(), reachable.end(), node) != reachable.end())
continue;
reachable.push_back(node);
for (auto next_node : get_successors(node))
todo.push_back(next_node);
}
return reachable;
}
Next, similarly to the pseudocode, we will assign to each block from reachable_sons that same list as dominators of that node, later we will go discarding the blocks, finally the only dominator for the head node will be the head node itself (because it is a reflexive relation). We include all those nodes in a set to apply the dominance analysis in all of them:
for (auto node : nodes)
dominators[node] = nodes;
dominators[head] = {head};
std::set<KUNAI::MJOLNIR::irblock_t> todo;
for (auto &node : nodes)
todo.insert(node);
Then we have the key of the algorithm. First, we retrieve from the set the node to analyze, and we need to calculate all the predecessors of that node with a function called get_predecessors, for each predecessor, we have to calculate the intersection of their dominators (those they have in common). For example, if we have the predecessors p1, p2, p3 and p4, we will take the dominators of p1 we call it dom(p1), then we will apply the intersection between dom(p1) and dom(p2), so we will take just those elements in common, then the same with p3 (dom(p1) Inter dom(p2)) Inter dom(p3), finally the same with p4. To the resulting list we will add the analyzed node itself, and in case the final list is different to the original dom(node), we have the resulting dominators list from node, then we add all the successors from node and we add them to the ToDo list:
while (!todo.empty())
{
auto node_it = todo.begin();
auto node = *node_it;
todo.erase(node_it);
if (node == head)
// do not use head for computing dominators
continue;
// computer intersection of all predecessors'dominators
Nodes new_dom = {};
for (auto pred : get_predecessors(node))
{
if (std::find(nodes.begin(), nodes.end(), pred) == nodes.end()) // pred is not in nodes
continue;
if (new_dom.empty())
new_dom = dominators[pred];
Nodes intersect_aux;
std::set_intersection(new_dom.begin(), new_dom.end(),
dominators[pred].begin(), dominators[pred].end(),
std::inserter(intersect_aux, intersect_aux.begin()));
new_dom = intersect_aux;
}
new_dom.push_back(node);
if (new_dom == dominators[node])
continue;
dominators[node] = new_dom;
for (auto succ : get_successors(node))
todo.insert(succ);
}
And finally, our map will contain for each node, the list of dominators! Pseudocode commonly uses mathematical notation, and it is common that algorithms expressed with this notation use things like recursion, but in languages like C++ using this can make memory usage grow because each call to the same function will create a new stack, and more memory will be used.
We can read one example of using this algorithm by Tim Blazytko - Introduction to Control-flow Graph Analysis.
Post-dominators
Another concept we have is the post-dominators. We say that a node p postdominates a node i, written p pdom i, if every possible execution path from i to exit node includes p, this is the same that saying i dom p in a CFG with all the edges reversed and entry and exit interchanged. Next I post the pseudocode algorithm from the paper Generalized Dominators and Post-dominators.

This time the function that implements the algorithm instead of receiving as a parameter the head of the CFG, it receives a leaf from the CFG:
std::map<irblock_t, Nodes> compute_postdominators(irblock_t leaf);
And now we reverse the calls, where we called reachable_sons now we call reachable_parents, where we had a call to get_predecessors we will have a call to get_successors, and vice versa.
First of all from the leaf retrieve all the parents, this is a call that calls the function reachable_nodes_backward which retrieves the predecessors, and the predecessors of the predecessors, etc.:
Nodes IRGraph::reachable_parents(irblock_t leaf)
{
return IRGraph::reachable_nodes_backward(leaf);
}
Nodes IRGraph::reachable_nodes_backward(irblock_t leaf)
{
Nodes todo;
Nodes reachable;
todo.push_back(leaf);
while (!todo.empty())
{
// similar to python pop.
auto node_it = todo.begin();
auto node = *node_it;
todo.erase(node_it);
// node already in reachable
if (std::find(reachable.begin(), reachable.end(), node) != reachable.end())
continue;
reachable.push_back(node);
for (auto next_node : get_predecessors(node))
todo.push_back(next_node);
}
return reachable;
}
After getting all the reachable parents, the algorithm assigns to all the nodes from the list, that list as post-dominators, assigning to the provided leaf node that same node as post-dominator.
std::map<irblock_t, Nodes> IRGraph::compute_postdominators(irblock_t leaf)
{
std::map<irblock_t, Nodes> postdominators;
auto nodes = reachable_parents(leaf);
for (auto node : nodes)
postdominators[node] = nodes;
postdominators[leaf] = {leaf};
Then, as we did with dominators, we must create a ToDo list to go through the nodes calculating the post-dominators from each node. This time, for the analyzed node, we will retrieve the successors, and we will apply the intersection of their post-dominators, then once we have applied the intersection to all the post-dominators of the successors, we add the node itself as a post-dominator, and we add its predecessors to the ToDo list. And with that, we will have the post-dominators algorithm!
Nodes todo = nodes;
while (!todo.empty())
{
auto node_it = todo.begin();
auto node = *node_it;
todo.erase(node_it);
if (node == leaf)
// do not use head for computing dominators
continue;
// computer intersection of all predecessors'dominators
Nodes new_dom = {};
for (auto succ : get_successors(node))
{
if (std::find(nodes.begin(), nodes.end(), succ) == nodes.end()) // pred is not in nodes
continue;
if (new_dom.empty())
new_dom = postdominators[succ];
Nodes intersect_aux;
std::set_intersection(new_dom.begin(), new_dom.end(),
postdominators[succ].begin(), postdominators[succ].end(),
std::inserter(intersect_aux, intersect_aux.begin()));
new_dom = intersect_aux;
}
new_dom.push_back(node);
if (new_dom == postdominators[node])
continue;
postdominators[node] = new_dom;
for (auto pred : get_predecessors(node))
todo.push_back(pred);
}
Immediate Dominators
Before I wrote about the definition of dominators, but we can define a subrelation called immediate dominance (known as idom) such that for a node a different to node b, a idom b if and only if a dom b and it does not exist a node c different to a and different to b, for which a dom c and c dom b, so a dominator of b such that there’s not another dominator node in the middle (for that reason immediate…). And we write it as idom(b). This dominator is an immediate dominator and is clearly unique, and the relation forms a tree of the nodes of a flow-graph whose root is the entry node, whose edges are the immediate dominances, and whose paths display all the dominance relationship. I think this explanation by Muchnick is clear enough. We can see the generated tree of immediate dominators in the next image:
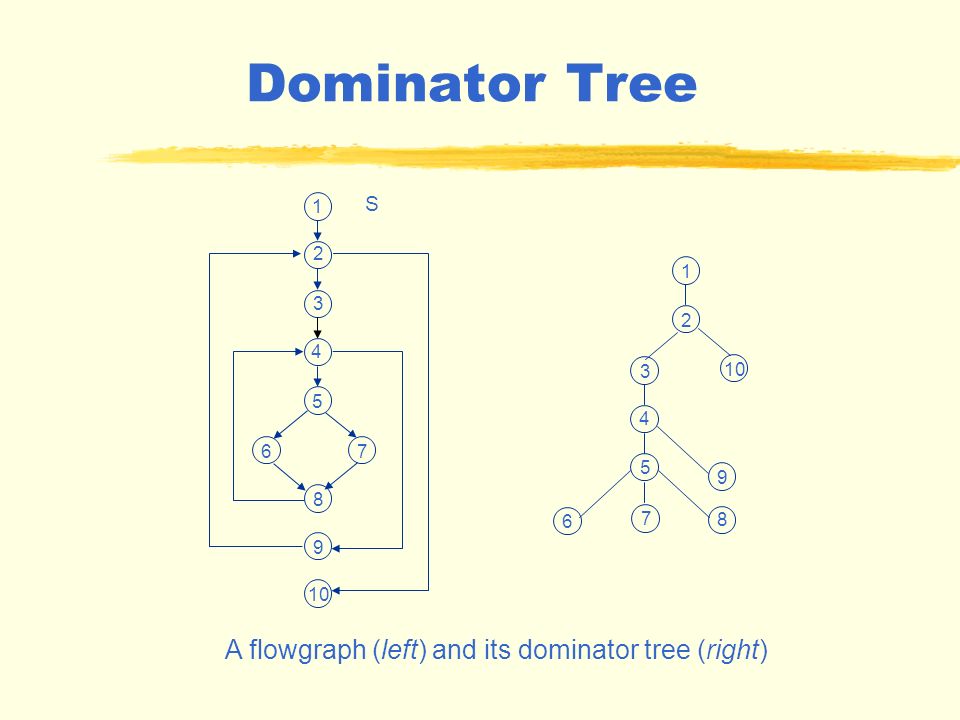
Muchnick for calculating the immediate dominators use the previously calculated dominators, we can see it in the next pseudocode:

This time MjolnIR’s function to calculate immediate dominators, returns a map, but the map is only a pair of nodes to map one node with its immediate dominator:
std::map<irblock_t, irblock_t> compute_immediate_dominators();
The first thing we do for calculating the immediate dominators is calculating the dominators as we have already seen in the pseudocode:
std::map<irblock_t, irblock_t> IRGraph::compute_immediate_dominators()
{
std::map<irblock_t, Nodes> tmp;
std::map<irblock_t, irblock_t> idom;
if (nodes.size() == 0)
return idom;
auto first_node = nodes[0];
// compute the dominators
tmp = compute_dominators(first_node);
Then, from the list of dominators of each node, we remove the node itself from that list:
// remove itself from dominators
for (auto &item : tmp)
{
auto rem = std::find(item.second.begin(), item.second.end(), item.first);
if (rem != item.second.end())
item.second.erase(rem);
}
The algorithm then takes a node for the analysis. From that node, we will use the dominator list of its dominators to obtain the immediate dominators. We can clearly see it with an example from Muchnick’s book, first we have a list of dominators for each node:
Now, we go to B1, from B1 from the list of dominators of B1 ({entry}) we will remove the dominators from its dominators (in this case entry), because the list of its dominators is empty, the idom(B1) is {entry}. Now we go with B2, we have its list of dominators {entry, B1}, now we will go over the dominators list of its dominators (B1 and entry) and we will remove the node that appears in those lists. The current dom(B1) now it is only {entry}, and we have that dom(B2) = {entry, B1}, we remove {entry} and we have that dom(B2) = {B1}, because the dom(entry) is empty, the algorithm is finished. We apply the same algorithm with all the next nodes. The C++ code for this is as follows:
for (auto n : nodes)
{
for (auto s : tmp[n])
{
for (auto t : tmp[n])
{
if (t == s)
continue;
if (std::find(tmp[s].begin(), tmp[s].end(), t) != tmp[s].end())
{
auto rem = std::find(tmp[n].begin(), tmp[n].end(), t);
if (rem != tmp[n].end())
tmp[n].erase(rem);
}
}
}
}
Finally, if the tmp list is not empty, we have that the last node from that list of dominators will be the immediate dominator. In the example from Muchnick we have the next final list:

We implement it in C++ like so:
for (auto n : nodes)
{
if (tmp[n].size() >= 1)
idom[n] = tmp[n][tmp[n].size() - 1];
else
idom[n] = nullptr;
}
The idom map contains for each node the immediate dominators.
We can go again to Tim Blazytko’s blog again, and see how to use immediate dominators for Automated Detection of Control-flow Flattening.
Immediate Post-dominators
Similarly to Immediate Dominators, we have the concept of Immediate Post-Dominators. The algorithm is basically the same but getting the post-dominators instead of the dominators, so here we can just check the algorithm with the explanation from the previous point:
std::map<irblock_t, irblock_t> IRGraph::compute_immediate_postdominators()
{
std::map<irblock_t, Nodes> tmp;
std::map<irblock_t, irblock_t> ipdom;
if (nodes.size() == 0)
return ipdom;
// compute post dominators
auto last_node = nodes.back();
tmp = compute_postdominators(last_node);
// remove itself from postdominators
for (auto &item : tmp)
{
auto rem = std::find(item.second.begin(), item.second.end(), item.first);
if (rem != item.second.end())
item.second.erase(rem);
}
for (auto &n : nodes)
{
for (auto &s : tmp[n]) // get the post dominators
{
for (auto &t : tmp[n]) // get again the post dominators except for s
{
if (t == s)
continue;
if (std::find(tmp[s].begin(), tmp[s].end(), t) != tmp[s].end())
{
auto rem = std::find(tmp[n].begin(), tmp[n].end(), t);
if (rem != tmp[n].end())
tmp[n].erase(rem);
}
}
}
}
for (auto n : nodes)
{
if (tmp[n].size() >= 1)
ipdom[n] = tmp[n][tmp[n].size() - 1];
else
ipdom[n] = nullptr;
}
return ipdom;
}
Dominance Frontier
We can find this concept in the paper Efficiently Computing Static Single Assignment Form and the Control Dependence Graph by Cytron et al. We have that a dominance frontier (commonly written as DF(X)) of a CFG node X is the set of all CFG nodes Y such that X dominates a predecessor of Y but does not strictly dominate Y. What does “Strictly dominate” mean? We can return to Muchnick, after explaining immediate dominators it says “We say that d strictly dominates i, written d sdom i, if d dominates i and d is different to i”. This algorithm of Dominance Frontier is commonly used to place the Phi functions (already explained in the instructions for MjolnIR). Next, the pseudocode of Dominance Frontier by Cytron et al.

Now we will see the algorithm in MjolnIR used to obtain the dominance frontier; the algorithm is a C++ version of the one used in Miasm.
First of all, the algorithm computes the immediate dominators, with the immediate dominator tree. It will be easy to see which nodes dominate one of the analyzed node’s predecessors, and do not strictly dominate the analyzed node.
std::map<irblock_t, std::set<irblock_t>> IRGraph::compute_dominance_frontier()
{
/*
* Compute the immediate dominators from all the
* nodes.
*/
auto idoms = compute_immediate_dominators();
Since the Dominance Frontier will be used to detect places where to write phi instructions, we will need to get the dominance frontier from the convergence nodes (those with two or more predecessors). The way we do that is checking the predecessors from the nodes from the idom tree:
for (auto &idom : idoms)
{
if (predecessors.find(idom.first) == predecessors.end() || predecessors.at(idom.first).size() < 2)
continue;
Then, we go through the predecessors from the analyzed node (idom.first the key from the map of immediate dominators). For each predecessor we will check if it is in the idoms tree. Then we will go through the idom tree from the current node, and from the predecessors. Inside of this loop we have to check if we are in a loop, because we are using predecessors. If we are in a loop, this loop would run forever. After that, we add in the frontier of the predecessor the current analyzed node, and we take the idom from the current predecessor as the new predecessor.
for (auto predecessor : predecessors[idom.first])
{
if (idoms.find(predecessor) == idoms.end())
continue;
while (predecessor != idom.second)
{
if (frontier[predecessor].find(idom.first) != frontier[predecessor].end())
break;
frontier[predecessor].insert(idom.first);
predecessor = idoms[predecessor];
}
}
We will later use this frontier to calculate where to write the phi nodes when moving from the current IR to an SSA-form.
Depth-First Search
After explaining a few complicated algorithms, we will move to something simpler. Depth-First search, and Breadth-First Search, these algorithms are useful to go through the control-flow graph using two different approaches. While in MjolnIR these two algorithms are used to retrieve the list of nodes sorted, in Muchnick’s book these are used to apply transformations before or after visiting the nodes. Four different transformations are explained:
- Process_Before() to perform an action before visiting each node.
- Process_After() to perform an action after visiting each node.
- Process_Succ_Before() to perform an action before visiting each successor of a node.
- Process_Succ_After() to perform an action after visiting each successor of a node.
In the case of Depth-First Search, the algorithm visits the descendents of a node in the graph before visiting any of its siblings that are not also descendents.
Next the algorithm by Muchnick:

The algorithm is easy to implement using an iterative algorithm, we create a ToDo list for the analysis with the head of the graph. From the ToDo list we will take the nodes from the back of the list, in that way we always go to the successors. Finally, we retrieve the successors, and we add it to the ToDo list in reverse order, so once we obtain the back from the ToDo list, we will retrieve the first successor.
Nodes IRGraph::Depth_First_Search(irblock_t head)
{
std::list<irblock_t> todo;
Nodes done;
todo.push_back(head);
while (!todo.empty())
{
// pop last element
auto node = todo.back();
todo.pop_back();
if (std::find(done.begin(), done.end(), node) != done.end())
continue;
done.push_back(node);
// push the nodes in reverse order
// so we go from left to right in depth
auto succs = get_successors(node);
for (auto succ = succs.rbegin(); succ != succs.rend(); ++succ)
todo.push_back(*succ);
}
return done;
}
Breadth-First Search
Next, we have the Breadth-First Search. In this algorithm, all nodes that are immediate descendants are processed before any of their unprocessed descendants. Next is Muchnick’s algorithm using recursion:

And a visual representation of how visiting a tree using a breadth-first search algorithm is:
Now the implementation in C++, this is even simpler to the previous one, we just create a list with the head of the graph, and then retrieve the successors and add it to the list , in that way we will always go in a breadth-first order:
Nodes IRGraph::Breadth_First_Search(irblock_t head)
{
std::list<irblock_t> todo;
Nodes done;
todo.push_back(head);
while (!todo.empty())
{
// pop first element
auto node = todo.front();
todo.pop_front();
if (std::find(done.begin(), done.end(), node) != done.end())
continue;
done.push_back(node);
for (auto succ : get_successors(node))
todo.push_back(succ);
}
return done;
}
Cyclomatic Complexity
This metric by Thomas J. McCabe allows to know the complexity of a program, or in the case of MjolnIR, to detect the complexity of a Dalvik method using the IR. We can consult it in wikipedia for example, where we can find an equation for the complexity: M = E - N + 2P, where M is the complexity, E the number of edges, N the number of nodes in the graph and P the number of connected components.
The implementation of MjolnIR is based on the implementation from Radare2, to calculate the strongly connected components, we just count those nodes that contain a return statement:
const std::uint64_t IRGraph::get_cyclomatic_complexity()
{
if (cyclomatic_complexity != -1)
{
return cyclomatic_complexity;
}
auto logger = LOGGER::logger();
// take a copy of nodes and edges
auto &nodes_aux = nodes;
auto &edges_aux = edges;
auto E = edges_aux.size();
auto N = nodes_aux.size();
size_t P = 0;
// Go through all the nodes to calculate those
// which are exit nodes
for (auto node : nodes_aux)
{
auto statements = node->get_statements();
// check all instructions
for (auto stmnt : statements)
{
if (ret_ir(stmnt))
{
P += 1;
break;
}
}
}
cyclomatic_complexity = E - N + P * 2;
logger->info("Calculated cyclomatic complexity: {}", cyclomatic_complexity);
return cyclomatic_complexity;
}
Reaching Definition
Before explaining something like def-use/use-def chains I need to define the concept of reading definition. Again, we will go to Muchnick’s book to know what is this reaching definition. First of all, a definition is an assignment of some value to a variable. We say the definition reaches a given point in a method if there is an execution path from the definition to that point such that the variable may have, at that point, the value assigned by the definition. This is, from the definition, to the selected point, there’s not a redefinition of the value. The next picture shows a very simple pseudocode of that algorithm from the next link https://www.csd.uwo.ca/~mmorenom/CS447/Lectures/CodeOptimization.html/node7.html:

This analysis is a bit more complex, so I implemented in MjolnIR it in a whole class. First of all, the algorithm involves creating a few types to store certain data. For example, we will have blockinstrtuple_t that is used to store the id of a basic block, and the id of an instruction:
using blockinstrtuple_t = std::tuple<
std::uint32_t, // block id
std::uint32_t // instruction id
>;
This tuple of data is used for storing something I called regdefinitionmap_t which stores the register or temporal register or whatever is defined as an IRExpr and the place where it is defined:
using regdefinitionmap_t = std::map<
irexpr_t, // reg or temp reg
blockinstrtuple_t>;
Finally, MjolnIR’s code contains a set of regdefinitionmap_t called regdefinitionset_t, and each instruction blockinstrtuple_t will contain a regdefinitionset_t in a type called reachingdeftype_t:
using reachingdeftype_t = std::map<
blockinstrtuple_t,
regdefinitionset_t>;
Next, the definition of the functions that will compute the reaching definition, the analysis involves understanding what the instructions do, since different instructions can be used to define a value.
class ReachingDefinition {
...
/**
* @brief Compute the reaching definition of the IRGraph given
* for each line we will have a definition of where variables
* are defined, and this is nice, because it will be useful
* to calculate the def-use and use-def chains.
*
*/
void compute();
/**
* @brief Analyze a block looking for definitions and updating the global
* reaching definitions object.
*
* @param block block to analyze.
*/
bool analyze_block(irblock_t &block);
/**
* @brief Analyze the given instruction, checking if the instruction create
* a definition, in case a definition exists, update the set of definitions.
*
* @param block current analyzed block
* @param instruction_id index of the instruction to analyze
* @return true
* @return false
*/
bool analyze_instruction(irblock_t &block, std::uint32_t instruction_id);
/**
* @brief Check if the given instruction is an instruction where there is some
* kind of definition or redefinition of a register, in that case return
* the reference of the register, in other case use optional to return
* a std::nullopt value.
*
* @param instr
* @return std::optional<irexpr_t&>
*/
std::optional<irexpr_t> is_reg_defined(irstmnt_t &instr);
}
The first thing we will do for computing the reaching definition on each line from the IR code will be to get the blocks in a Depth-First search order, then we will call analyze_block for each block. We will do this while new definitions are found:
void ReachingDefinition::compute()
{
bool change = true;
auto dfs = graph->Depth_First_Search(graph->get_nodes()[0]);
while (change)
{
change = false;
for (auto &block : dfs)
change |= analyze_block(block);
}
}
For doing the analysis of each block, what we will do first is to generate the list of input definitions of the current block, that we will call in(w), this list is created with the output definitions from the predecessors of the current block, we will call each list of the out definitions from each predecessor out(p), then we will have that in(w) = U out(p) for each p in predecessor(w). The list out(p) are the definitions in the last instruction of the block (these lists will be empty at the beginning of the execution, for that reason the algorithm runs iterations until no more changes appear). This is the implementation of in(w) = U out(p) for each p in predecessor(w) in C++:
bool ReachingDefinition::analyze_block(irblock_t &block)
{
regdefinitionset_t predecesor_state;
bool modified;
// Go through each predecessor of the current block
// in(w) = U out(p) for p in pred(w)
for (auto pred : graph->get_predecessors(block))
{
// take the set of definitions from the last instruction of previous block
auto &lval_definitions = reaching_definitions[std::make_tuple(pred->get_start_idx(), pred->get_number_of_statements())];
// add it to predecesor state
for (auto &lval_definition : lval_definitions)
predecesor_state.insert(lval_definition);
}
Then detect if there was a modification, that means checking if previously in(w) didn’t exist, or if the calculated in(w) is different to a previous in(w) from another iteration. For doing that, we need to do checking with the previously seen reaching_definitions variable, which contains all the reaching definition values. If no modification exists, return false:
modified = (reaching_definitions.find(std::make_tuple(block->get_start_idx(), 0)) == reaching_definitions.end()) || (reaching_definitions[std::make_tuple(block->get_start_idx(), 0)] != predecesor_state);
if (!modified)
return false;
Now, we save this new in(w) in the reaching_definitions variable:
reaching_definitions[std::make_tuple(block->get_start_idx(), 0)] = predecesor_state;
Now that we have in(w) we need to analyze each instruction looking for definitions, a definition in a new instruction, kills a definition in a previous instruction if they are defining the same value. We do it with a loop and calling analyze_instruction:
for (size_t index = 0, size = block->get_number_of_statements(); index < size; index++)
modified |= analyze_instruction(block, index);
return modified;
And here we would have finished the analysis of the blocks. Now we can move to the analysis of the instructions.
First of all, we obtain the definitions that come to the current instruction, we need the next defs = in(instr):
bool ReachingDefinition::analyze_instruction(irblock_t &block, std::uint32_t instruction_id)
{
bool modified;
irstmnt_t &instr = block->get_statements().at(instruction_id);
// defs = in(instr)
auto defs = reaching_definitions[std::make_tuple(block->get_start_idx(), instruction_id)];
Now we need to retrieve if the current instruction generates a new definition of a variable (register in this case), and in case there’s a definition we need to update the list of out(instruction) which are the definitions that goes out from this instruction, we can express it in the next way: out(instr) = gen(instr) U (in(instr) - kill(instr)), the output generations are, the current generations joined with the generations that comes from previous instructions without taking in consideration those definitions that were killed by the current one! We will obtain if a register is defined calling is_reg_defined. All of this, is translated into C++ in the following way:
auto reg_defined = is_reg_defined(instr);
if (reg_defined)
{
// out(instr) = gen(instr) U (in(instr) - kill(instr))
// in(instr) - kill(instr)
for (auto it = defs.begin(); it != defs.end(); it++)
{
const auto& map_value = *it;
if (map_value.find(reg_defined.value()) != map_value.end())
// we are going to remove previous definitions
// of the same registers
it = defs.erase(it);
}
// gen(instr)
defs.insert();
}
Finally, to know if we have some modification, we have to compare the current out(instruction) with the previously stored out(instruction), and in case there’s some modification we store this new out(instruction) (which is the same as in(instruction+1)), and return true!
// old out(instr) == out(instr)?
modified = (reaching_definitions.find(std::make_tuple(block->get_start_idx(), instruction_id + 1)) == reaching_definitions.end()) || reaching_definitions[std::make_tuple(block->get_start_idx(), instruction_id + 1)] != defs;
if (modified)
// in(instr+1) = out(instr)
reaching_definitions[std::make_tuple(block->get_start_idx(), instruction_id + 1)] = defs;
return modified;
}
And how does is the is_reg_defined function look? It’s just a function that checks the type of instruction, checks if a register is defined, and then returns that register:
std::optional<irexpr_t> ReachingDefinition::is_reg_defined(irstmnt_t &instr)
{
irexpr_t reg;
// A = B
if (auto assign_instr = assign_ir(instr))
{
reg = assign_instr->get_destination();
}
// A = IRUnaryOp B
else if (auto unary_instr = unary_op_ir(instr))
{
reg = unary_instr->get_result();
}
// A = B IRBinaryOp C
else if (auto bin_instr = bin_op_ir(instr))
{
reg = bin_instr->get_result();
}
// A = load(MEM)
else if (auto load_instr = load_ir(instr))
{
reg = load_instr->get_destination();
}
// A = New Class
else if (auto new_instr = new_ir(instr))
{
reg = new_instr->get_result();
}
// A = New Array
else if (auto alloca_instr = alloca_ir(instr))
{
reg = alloca_instr->get_result();
}
// A = phi(A, A, A...)
else if (auto phi_instr = phi_ir(instr))
{
reg = phi_instr->get_result();
}
else
return std::nullopt;
return reg;
}
In this way, we loop until no more definitions exist, and with all these algorithms we will have the definitions from the program, where the definitions were done, and until when these definitions exist.
For seeing a python implementation, I highly recommend going to the following code from Miasm, also as stated in their comment, I recommend reading the paper A survey of data flow analysis techniques. by Kennedy, K. (1979).
Def-Use/Use-Def chains
Finally, we arrive to an important concept from the analysis of IRs which are the def-use and the use-def chains. We previously defined the definitions as any point where a value is set in a variable. On the other side, we have uses, which are points in the graph where a variable with a definition is used. These two concepts are also referred as Du-Chains and Ud-Chains in Muchnick’s book. Du-Chains for a variable connects a definition of that variable to all the uses it may flow to, while a ud-chain connects a use to all the definitions that may flow to it. The complexity of this analysis is in detecting where a definition is used without being redefined, and which are the definitions connected to a usage. Although we haven’t seen the implementation of the SSA form yet, it is useful saying that things like Def-Use and Use-Def chains are much easier to implement than in an IR without an SSA form. In SSA each variable can be defined just once, so for each variable we will have only one definition and multiple uses. If we do not use SSA, each variable can have multiple definitions.
For understanding how are def-use and use-def chains, we can go to the following link from the Miasm Project use-def, they perfectly explain how the values of two parameters from a call can come from two previous blocks, in that case, for variable a we have two definitions as well as for b. But those definitions have as use the call(a,b). In that case, we would have the next def-use/use-def chain:
a = {def: lbl1.1, lbl2.1, use: lbl3.1}
b = {def: lbl1.2, lbl2.2, use: lbl3.1}
I also like the example they provide in the comment from their code which I highly recommend to read: miasm def-use/use-def.
"""
IR block:
lbl0:
0 A = 1
B = 3
1 B = 2
2 A = A + B + 4
Def use analysis:
(lbl0, 0, A) => {(lbl0, 2, A)}
(lbl0, 0, B) => {}
(lbl0, 1, B) => {(lbl0, 2, A)}
(lbl0, 2, A) => {}
"""
Now, I will go with the implementation from MjolnIR. The implementation of the computation of def-use and use-def chains was done in the class Optimizer both in optimizer.hpp and optimizer.cpp. For calculating these chains we will need three parameters, one IRGraph containing the method to analyze and reachingdefinition_t a reaching definition analysis output from the previous point. The next functions will calculate these chains:
class Optimizer {
...
/**
* @brief Calculate the def-use and use-def chains in an IRGraph
* for doing that we need to accept a reaching definition
* with the analysis already run. All the changes will be
* applied directly to the instructions of the IRGraph.
*
* @param ir_graph graph of a function in MjolnIR to calculate its def-use, use-def chains
* @param reachingdefinition the object with the reaching definition.
*/
void calculate_def_use_and_use_def_analysis(MJOLNIR::irgraph_t ir_graph,
reachingdefinition_t &reachingdefinition);
...
/**
* @brief Solve a def_use and use_def chain given an operand and a instruction
* here we will solve the reaching definition value and then we will cross-reference
* the instructions.
*
* @param operand
* @param expr
* @param reach_def_set
* @param ir_graph
*/
void solve_def_use_use_def(irexpr_t &operand, irstmnt_t expr, regdefinitionset_t &reach_def_set, MJOLNIR::irgraph_t ir_graph);
...
}
The first function calculate_def_use_and_use_def_analysis is the public function that will analyze the IRGraph and will do some kind of magic to collect the information. First of all we will go through the IRBlocks that belong to the graph, and as expected, from each block, we will go through the instructions (easy cheesy!):
void Optimizer::calculate_def_use_and_use_def_analysis(MJOLNIR::irgraph_t ir_graph,
reachingdefinition_t &reachingdefinition)
{
for (auto &block : ir_graph->get_nodes())
{
auto &instructions = block->get_statements();
for (size_t _size_instr = block->get_number_of_statements(), i = 0; i < _size_instr; i++)
{
After this, we will retrieve one of the instructions, and we will check if that index (block index, instruction index) contains a regdefinitionset_t (if you do not remember it, you can check it in the previous section). With this, we know if there’s some definitions in that instruction or not:
auto &instr = instructions.at(i);
auto reach_def_instr = reachingdefinition->get_reach_definition_point(block->get_start_idx(), i);
// check if there was a reach_def
if (!reach_def_instr.has_value())
continue;
auto reach_def_set = reach_def_instr.value();
// check if set is empty
if (reach_def_set.empty())
continue;
The reaching definitions will tell us where a defined register value will reach (for that reason reaching, and for that reason definition, again easy cheesy). Now we will apply the analysis to the different MjolnIR’s instructions, some of them define registers, some of them use them. In any case, we need to apply the function solve_def_use_use_def to all the used registers (not the defined ones). Next is the code that cast the IRStmnt and applies different code for each instruction type:
// A = B
if (auto assign_instr = assign_ir(instr))
{
assign_instr->invalidate_chains();
auto op = assign_instr->get_source();
solve_def_use_use_def(op, assign_instr, reach_def_set, ir_graph);
}
// A = phi(A1, A2, A3, ...)
else if (auto phi_instr = phi_ir(instr))
{
phi_instr->invalidate_chains();
auto& params = phi_instr->get_params();
for (auto& op : params)
solve_def_use_use_def(op.second, phi_instr, reach_def_set, ir_graph);
}
// A = IRUnaryOp B
else if (auto unary_op_instr = unary_op_ir(instr))
{
unary_op_instr->invalidate_chains();
auto op = unary_op_instr->get_op();
solve_def_use_use_def(op, unary_op_instr, reach_def_set, ir_graph);
}
// A = B IRBinaryOp C
else if (auto bin_op_instr = bin_op_ir(instr))
{
bin_op_instr->invalidate_chains();
auto op1 = bin_op_instr->get_op1();
auto op2 = bin_op_instr->get_op2();
solve_def_use_use_def(op1, bin_op_instr, reach_def_set, ir_graph);
solve_def_use_use_def(op2, bin_op_instr, reach_def_set, ir_graph);
}
// CALL (A,B,C,...)
else if (auto call_instr = call_ir(instr))
{
for (auto op : call_instr->get_args())
{
solve_def_use_use_def(op, call_instr, reach_def_set, ir_graph);
}
}
// A = *B[C]
else if (auto load_instr = load_ir(instr))
{
load_instr->invalidate_chains();
auto source = load_instr->get_source();
auto index = load_instr->get_index();
solve_def_use_use_def(source, load_instr, reach_def_set, ir_graph);
if (index)
solve_def_use_use_def(index, load_instr, reach_def_set, ir_graph);
}
// *B[C] = A
else if (auto store_instr = store_ir(instr))
{
store_instr->invalidate_chains();
auto source = store_instr->get_source();
solve_def_use_use_def(source, store_instr, reach_def_set, ir_graph);
}
// RET A
else if (auto ret_instr = ret_ir(instr))
{
ret_instr->invalidate_chains();
auto ret_value = ret_instr->get_return_value();
if (auto reg_value = expr_ir(ret_value))
solve_def_use_use_def(reg_value, ret_instr, reach_def_set, ir_graph);
}
// JCC <condition>
else if (auto jcc_instr = conditional_jump_ir(instr))
{
jcc_instr->invalidate_chains();
auto condition = jcc_instr->get_condition();
if (auto reg_value = expr_ir(condition))
solve_def_use_use_def(reg_value, jcc_instr, reach_def_set, ir_graph);
}
// BComp A, B
else if (auto bcomp_instr = bcomp_ir(instr))
{
bcomp_instr->invalidate_chains();
if (auto reg = bcomp_instr->get_reg1())
solve_def_use_use_def(reg, bcomp_instr, reach_def_set, ir_graph);
if (auto reg = bcomp_instr->get_reg2())
solve_def_use_use_def(reg, bcomp_instr, reach_def_set, ir_graph);
}
// ZComp A, 0
else if (auto zcomp_instr = zcomp_ir(instr))
{
zcomp_instr->invalidate_chains();
if (auto reg = zcomp_instr->get_reg())
solve_def_use_use_def(reg, zcomp_instr, reach_def_set, ir_graph);
}
// A = Alloca[REG]
else if (auto alloca_instr = alloca_ir(instr))
{
alloca_instr->invalidate_chains();
irstmnt_t size = alloca_instr->get_size();
if (irexpr_t reg = register_ir(size))
solve_def_use_use_def(reg, alloca_instr, reach_def_set, ir_graph);
}
MjolnIR had helper instructions that applied the casts, or returned nullptr in case the instruction was not the checked one, allowing the use of if code to enter or not to the condition. Also, we have register_ir to know if a provided value is a register or not. One interesting thing is that we find the call to the function invalidate_chains from IRStmnt that will delete the def-use and the use-def chain for each instruction.
void IRStmnt::invalidate_chains()
{
invalidate_use_def_chain();
invalidate_def_use_chains();
}
void invalidate_use_def_chain()
{
use_def_chain.clear();
}
void invalidate_def_use_chains()
{
def_use_chains.clear();
}
Let’s move to solve_def_use_use_def, here we got as parameters the operand, the expression with the instruction, the reaching definitions for that instruction and the graph with the whole method. What we do is pretty easy, we need to detect that the operand is in the reaching definition. If we detect it, we are detecting a use from a register, and with the reaching definition map we will detect where the value was defined. Then we will obtain the instruction where the register was defined and we do the next: in the definition instruction set a use for the defined register, in the current instruction set a definition for the used register.
void Optimizer::solve_def_use_use_def(irexpr_t &operand,
irstmnt_t expr,
regdefinitionset_t &reach_def_set,
MJOLNIR::irgraph_t ir_graph)
{
// we need to detect the operand in the reach definition
// and in case we find it, we will create the def-use and
// use-def chains.
for (auto &reach_def_map : reach_def_set)
{
// look for the operand in the Reaching definition
if (reach_def_map.find(operand) != reach_def_map.end())
{
auto &reach_def = reach_def_map.at(operand);
// extract where the operand was defined.
auto block = std::get<0>(reach_def);
auto instr = std::get<1>(reach_def);
auto definition_block = ir_graph->get_node_by_start_idx(block);
if (!definition_block.has_value())
continue;
// get the instruction, we will use it to cross-reference both
auto definition_instr = definition_block.value()->get_statements().at(instr);
// set one use of a definition
definition_instr->add_instr_to_use_def_chain(expr);
// set one definition of a use
expr->add_instr_to_def_use_chain(operand, definition_instr);
}
}
}
Then, we will have in each instruction the uses as a list of instructions where the defined value is used. And in the use instruction, we will have for the operand a list of definition instructions. IRStmnt has a method for printing these chains:
void IRStmnt::print_use_def_and_def_use_chain()
{
std::cout << "Use-Def and Def-Use chain of: " << this->to_string() << "\n";
if (!use_def_chain.empty())
{
std::cout << "\tUse-Def chain:\n";
for (auto &use_def : use_def_chain)
std::cout << "\t\t" << use_def->to_string() << "\n";
}
if (!def_use_chains.empty())
{
std::cout << "\tDef-Use chains:\n";
for (auto &def_use : def_use_chains)
{
auto &value = def_use.first;
std::cout << "\t\t" << value->to_string() << ": ";
for (auto &def : def_use.second)
std::cout << def->to_string() << "\n";
}
}
}
As I commented, for an SSA-form this will be simpler since only one definition exists with multiple uses. But for now, this is all!
MjolnIR - Analysis
Once we have seen all the graph algorithms, we can go to the usage of these algorithms. This section of the long post will have one larger subsection, and others are shorter because I couldn’t improve that part of the code in the past.
SSA Graph generation
As I previously said, there is a form of IR known as Static-Single Assignment Form (SSA Form). In this form, each time a variable is defined after an assignment, or after an operation that generates some result, a new variable is created, and that’s because variables can be assigned only once and used multiple times. This IR form was developed by IBM researchers in the 80s, and it became beneficial to apply optimizations in the IR. For example, an analysis as the def-use/use-def chains we previously saw, it becomes a single point of definition and then a list of uses, making this representation easy to obtain.
For obtaining this representation, there are algorithms that can be used to directly obtain this representation without obtaining an intermediate form of an IR, in this post a friend of mine and I explain this method used in a new version of MjolnIR: https://farena.in/compilers/mlir/ssa-mlir-algorithm/. But for the primitive version of MjolnIR I used the next Efficiently Computing Static Single Assignment Form and the Control Dependence Graph by Cytron et al., as I previously said. This is because MjolnIR with IRGraph already had an intermediate form of IR that I was able to use (and also because at that moment it was the only way I knew).
For constructing the SSA Graph a new class called IRGraphSSA exists, this class receives in the constructor an IRGraph as parameter, with this the new graph will be generated, with this, and with all the next functions:
/**
* @brief Obtain all kind of assignment that can generate
* a newer value for a variable.
*
* @param graph
*/
void collect_var_assign();
/**
* @brief Look for a place in the dominance frontier where
* to write
*
*/
void insert_phi_node();
/**
* @brief Apply variable renaming to a basic block of the IRGraph
* here we will apply the global variables in order to translate
* each instruction.
*
* @param v basic block to translate.
*/
void search(const irblock_t &v);
/**
* @brief Translate an instruction to an SSA form this will involve
* parsing the instruction and checking if it contains registers
* to translate to a new SSA form.
*
* @param instr instruction to translate to an SSA form
* @param p defined registers that we must remove later from stack.
* @return irstmnt_t
*/
irstmnt_t translate_instruction(irstmnt_t &instr, std::list<irreg_t> &p);
/**
* @brief Create a new register for the SSA, this will be used
* in the renaming algorithm, the algorithm is based in
* the one of the book
* "An Introduction to the Theory of Optimizing Compilers".
* This function will use both C and S.
*
* @param old_reg register we want to transform to SSA
* @param p defined registers that we must remove later from stack.
* @return irreg_t
*/
irreg_t create_new_ssa_reg(irreg_t old_reg, std::list<irreg_t> &p);
/**
* @brief Get the top of the S stack for a given register, in case
* it doesn't exist yet, call to create_new_ssa_reg function.
*
* @param old_reg register we want to transform to SSA
* @param p definedd registers that we must remove later from stack
* @return irreg_t
*/
irreg_t get_top_or_create(irreg_t old_reg, std::list<irreg_t> &p);
All these functions are used to do tasks like inserting phi instructions using the previously defined dominance frontier. Also, the algorithm needs to rename all the registers, adding a sub-index (e.g. from r0 we will need r0_1, r0_2, etc) for each assignment done to the register. Let’s move to the constructor of this class.
The first thing we do in the constructor is copying the nodes and the edges, as well as calculating the dominance tree (calculating the immediate dominators).
IRGraphSSA::IRGraphSSA(irgraph_t &code_graph)
{
auto nodes = code_graph->get_nodes();
auto edges = code_graph->get_edges();
for (auto node : nodes)
add_node(node);
for (auto edge : edges)
add_edge(edge.first, edge.second);
dominance_tree = compute_immediate_dominators();
- collect_var_assign Analysis
Then the algorithm calls to collect_var_assign, this function simply collects for each register the blocks where a definition exists. First of all let’s see the call to that function:
IRGraphSSA::IRGraphSSA(irgraph_t &code_graph)
{
...
collect_var_assign();
...
}
And now what this function does:
void IRGraphSSA::collect_var_assign()
{
auto &blocks = get_nodes();
for (auto &block : blocks)
{
auto &instrs = block->get_statements();
for (auto &instr : instrs)
{
// A = B
if (auto assign_instr = assign_ir(instr))
{
irstmnt_t destination = assign_instr->get_destination();
if (auto reg = register_ir(destination))
{
var_block_map[reg].insert(block);
continue;
}
}
// A = IRUnaryOp B
else if (auto unary_instr = unary_op_ir(instr))
{
irstmnt_t result = unary_instr->get_result();
if (auto reg = register_ir(result))
{
var_block_map[reg].insert(block);
continue;
}
}
// A = B IRBinaryOp C
else if (auto binary_instr = bin_op_ir(instr))
{
irstmnt_t result = binary_instr->get_result();
if (auto reg = register_ir(result))
{
var_block_map[reg].insert(block);
continue;
}
}
// A = LOAD(B[INDEX])
else if (auto load_instr = load_ir(instr))
{
irstmnt_t destination = load_instr->get_destination();
if (auto reg = register_ir(destination))
{
var_block_map[reg].insert(block);
continue;
}
}
// A = New Class
else if (auto new_ir_instr = new_ir(instr))
{
irstmnt_t result = new_ir_instr->get_result();
if (auto reg = register_ir(result))
{
var_block_map[reg].insert(block);
continue;
}
}
// call <callee>(arg1, arg2, arg3...)
else if (auto call_instr = call_ir(instr))
{
irstmnt_t ret_val = call_instr->get_ret_val();
// it can be void call
if (ret_val == nullptr)
continue;
if (auto reg = register_ir(ret_val))
{
var_block_map[reg].insert(block);
continue;
}
}
// STORE(A) = B
else if (auto store_instr = store_ir(instr))
{
irstmnt_t destination = store_instr->get_destination();
if (auto reg = register_ir(destination))
{
var_block_map[reg].insert(block);
continue;
}
}
// A = Alloca(B)
else if (auto alloca_instr = alloca_ir(instr))
{
irstmnt_t result = alloca_instr->get_result();
irstmnt_t size = alloca_instr->get_size();
if (auto reg = register_ir(result))
{
var_block_map[reg].insert(block);
}
if (auto reg = register_ir(size))
{
var_block_map[reg].insert(block);
}
continue;
}
}
}
}
- insert_phi_node Analysis
So now, we should clearly see all the instructions that produce some register as a result. All of those registers are key for a map called var_block_map that will keep the blocks where the definitions exist. We will use that list right now for inserting the phi, because after calling collect_var_assign, the constructor calls insert_phi_node:
IRGraphSSA::IRGraphSSA(irgraph_t &code_graph)
{
...
insert_phi_node();
...
}
Let’s take a look to insert_phi_node, the first thing the algorithm does is to calculate the dominance frontier, it will be used to detect if a phi node must be inserted:
void IRGraphSSA::insert_phi_node()
{
Nodes work_list;
std::list<irblock_t> seen;
std::unordered_map<irblock_t, irreg_t> inserted;
auto dominance_frontier = compute_dominance_frontier();
Now, we will loop through the var_block_map previously created, we will take the register from the key as the current register to analyze, and we will create a work list with all the blocks where the register is defined, this work list will be complemented with the seen list to avoid analyzing a block twice:
for (const auto &p : var_block_map)
{
const irreg_t ® = p.first;
for (auto &block : p.second)
work_list.push_back(block);
We will retrieve the dominance frontier for each block, and for each one of those blocks in the dominance frontier we will add a phi instruction, we will add the result register where we assign the final value, but we will have to wait until the end of IRGraphSSA constructor to assign the parameters to that phi instruction, and to remove the phi values that are not needed (optimization of phi nodes).
while (!work_list.empty())
{
auto &block = work_list.front();
work_list.erase(work_list.begin());
seen.push_back(block);
for (auto &df_block : dominance_frontier[block])
{
if (inserted[df_block] != reg)
{
// add phi node
inserted[df_block] = reg;
auto phi_instr = std::make_shared<IRPhi>();
phi_instr->add_result(reg);
df_block->add_statement_at_beginning(phi_instr);
df_block->set_phi_node();
if (std::find(seen.begin(), seen.end(), df_block) == seen.end())
// finally add the block from dominance_frontier
// into the worklist
work_list.push_back(df_block);
}
}
}
- Return to IRGraphSSA constructor
Finally, we will call a function called search, that we will later analyze, for both the nodes without predecessors (for example those from catch blocks), and the first node:
IRGraphSSA::IRGraphSSA(irgraph_t &code_graph)
{
...
auto &first_node = get_nodes()[0];
for (auto & node : get_nodes())
{
if (get_predecessors(node).size() == 0 && node != first_node)
search(node);
}
search(first_node);
}
- Renaming the registers
Now that we have the phi instructions in the dominance frontiers, we will apply renaming to the registers, and we will fill the phi instructions with registers for the parameters. Before digging deeper into the search function, let’s see two functions that are used for creating the new registers, these new registers are based in the number of the previous registers, but they include a new sub-index. For storing them, I used a stack, and I was able to retrieve the last generated register, or create a new one with a newer sub-index:
irreg_t IRGraphSSA::get_top_or_create(irreg_t old_reg, std::list<irreg_t> &p)
{
if (S.find(old_reg) != S.end() && S[old_reg].size() != 0)
return S[old_reg].top();
else
return create_new_ssa_reg(old_reg, p);
}
irreg_t IRGraphSSA::create_new_ssa_reg(irreg_t old_reg, std::list<irreg_t> &p)
{
irreg_t new_reg;
if (C.find(old_reg) == C.end())
C[old_reg] = 0;
new_reg = std::make_shared<IRReg>(old_reg->get_id(),
C[old_reg],
old_reg->get_current_arch(),
old_reg->to_string() + "." + std::to_string(C[old_reg]),
old_reg->get_type_size());
// save last index of the register
C[old_reg]++;
// save all the references to new registers
// from old one
S[old_reg].push(new_reg);
// save the old register from the newer one
ssa_to_non_ssa_form[new_reg] = old_reg;
p.push_back(old_reg);
return new_reg;
}
As we can appreciate, S is used to store the new registers given the old one, C keeps for each old register, the last sub-index used, and finally we also have a map for translating from a new register to an old one (ssa_to_non_ssa_form). Finally, we can start with search function.
First of all, the function will go through each instruction from the block, each statement will be processed and translated to an SSA-form. In some case, like it could be some phi instructions, the translation will return null, and in that case we can annotate the instruction as an instruction to be removed. In another case, what we will have is a new instruction to be inserted in the list of statements.
void IRGraphSSA::search(const irblock_t &v)
{
// defined registers in the block
std::list<irreg_t> p;
// instructions to remove
std::stack<size_t> to_remove;
auto &statements = v->get_statements();
// process each statement of the block
for (size_t v_size = statements.size(), i = 0; i < v_size; i++)
{
auto &instr = statements[i];
auto new_instr = translate_instruction(instr, p);
// check if the instruction have been removed
if (new_instr == nullptr)
{
to_remove.push(i);
continue;
}
if (new_instr != instr)
statements[i] = new_instr;
}
Next, it is time to remove all the instructions from the statement list:
// remove from vector in post order
while(!to_remove.empty())
{
auto index = to_remove.top();
to_remove.pop();
statements.erase(statements.begin() + index);
}
Then, we need to go through the phi instructions from the successors. Since we have translated the instructions, we know which are the last registers that have been created using SSA form, so if we find in a successor a phi instruction that as a result has one of the registers we have converted to SSA, it means that the Phi instruction receives as one of the parameters that new defined register (this is the trick why we also have ssa_to_non_ssa_form, to convert the registers to non-SSA form, and being able to discover if we can insert a parameter into phi :D). Finally, to know which position the parameter is, we see the position of the current analyzed block in the list of predecessors from the node with the phi instruction:
// process the phi statements from the successors
auto &succs = get_successors(v);
for (auto &w : succs)
{
// if the next block does not contain
// a phi node, just continue, avoid
// all the other calculations
if (!w->contains_phi_node())
continue;
// extract which_pred is v for w
// this will take by index which
// predecessor is v from w
auto &preds = get_predecessors(w);
auto it = find(preds.begin(), preds.end(), v);
int j = -1;
if (it != preds.end())
j = it - preds.begin();
// now look for phi functions.
auto &w_stmnts = w->get_statements();
for (auto &w_stmnt : w_stmnts)
{
if (auto phi_instr = phi_ir(w_stmnt))
{
// trick to fill the parameters from the PHI function
// extract the result register, and turn it to a non SSA form
// if needed, then assign the register to the phi statement
// as one of the parameters.
irreg_t reg = std::dynamic_pointer_cast<IRReg>(phi_instr->get_result());
if (reg->get_sub_id() != -1)
reg = ssa_to_non_ssa_form[reg];
if (S.find(reg) != S.end() && S[reg].size() > 0)
phi_instr->get_params()[j] = S[reg].top();
}
}
}
Finally, the search function will call itself with the next block to analyze, which is the next block to analyze? The one that is strictly dominated by the current one, and for that we calculated the dominance tree. In that way, we will go through all the blocks in a correct order. Finally, the algorithm pops all the registers defined in that block, finishing the algorithm for transforming the IRGraph into an IRGraphSSA:
// go through each child from the dominance tree
for (auto &doms : dominance_tree)
// check that current block strictly
// dominates the next one to analyze
if (doms.second == v)
{
auto &child = doms.first;
search(child);
}
// now POP all the defined variables here!
for (auto x : p)
S[x].pop();
}
- Translating the instructions to SSA
Each instruction will need to be handled differently to be translated to an SSA form, since each instruction uses the registers differently. For example an assignment can contain two registers, one source and one destination, if both operands are registers, we need to check if a previous SSA register exists for the source, and then create a new SSA register for the destination register. Here it is the code for doing that:
// A = B
if (auto assign_instr = assign_ir(instr))
{
irstmnt_t destination = assign_instr->get_destination();
irstmnt_t source = assign_instr->get_source();
if (auto reg = register_ir(source))
source = get_top_or_create(reg, p);
if (auto reg = register_ir(destination))
destination = create_new_ssa_reg(reg, p);
new_instr = std::make_shared<IRAssign>(std::dynamic_pointer_cast<IRExpr>(destination), std::dynamic_pointer_cast<IRExpr>(source));
}
Mostly, the translation of the instructions is: for the register operands we look for the last created register, or we create one; for the register sources, we create a new one.
The phi instruction is a different case, since the code from search already assigned the parameters from Phi instruction as SSA registers, so only the destination register is created. But if the phi instruction contains less than two parameters, it means that the phi instruction is not necessary, so we can remove it, we do that returning null as we previously saw in the search function:
// Phi node (only the result)
if (auto phi_instr = phi_ir(instr))
{
irstmnt_t result = phi_instr->get_result();
if (auto reg = register_ir(result))
result = create_new_ssa_reg(reg, p);
new_instr = std::make_shared<IRPhi>();
auto aux = std::dynamic_pointer_cast<IRPhi>(new_instr);
aux->add_result(std::dynamic_pointer_cast<IRExpr>(result));
for (auto param : phi_instr->get_params())
{
aux->add_param(param.second, param.first);
}
// not necessary a phi where we do not have
// more than one parameter
if (aux->get_params().size() < 2)
return nullptr;
}
For finishing this part, you can find here the whole method used for translating the instructions to an SSA form:
irstmnt_t IRGraphSSA::translate_instruction(irstmnt_t &instr, std::list<irreg_t> &p)
{
irstmnt_t new_instr = instr;
// A = B
if (auto assign_instr = assign_ir(instr))
{
irstmnt_t destination = assign_instr->get_destination();
irstmnt_t source = assign_instr->get_source();
if (auto reg = register_ir(source))
source = get_top_or_create(reg, p);
if (auto reg = register_ir(destination))
destination = create_new_ssa_reg(reg, p);
new_instr = std::make_shared<IRAssign>(std::dynamic_pointer_cast<IRExpr>(destination), std::dynamic_pointer_cast<IRExpr>(source));
}
// A = IRUnaryOp B
else if (auto unary_instr = unary_op_ir(instr))
{
irstmnt_t result = unary_instr->get_result();
irstmnt_t op = unary_instr->get_op();
if (auto reg = register_ir(op))
op = get_top_or_create(reg, p);
if (auto reg = register_ir(result))
result = create_new_ssa_reg(reg, p);
if (unary_instr->get_unary_op_type() == IRUnaryOp::CAST_OP_T && unary_instr->get_cast_type() == IRUnaryOp::TO_CLASS)
new_instr = std::make_shared<IRUnaryOp>(IRUnaryOp::CAST_OP_T, IRUnaryOp::TO_CLASS, unary_instr->get_class_cast(), std::dynamic_pointer_cast<IRExpr>(result), std::dynamic_pointer_cast<IRExpr>(op));
else if (unary_instr->get_unary_op_type() == IRUnaryOp::CAST_OP_T)
new_instr = std::make_shared<IRUnaryOp>(IRUnaryOp::CAST_OP_T, unary_instr->get_cast_type(), std::dynamic_pointer_cast<IRExpr>(result), std::dynamic_pointer_cast<IRExpr>(op));
else
new_instr = std::make_shared<IRUnaryOp>(unary_instr->get_unary_op_type(), std::dynamic_pointer_cast<IRExpr>(result), std::dynamic_pointer_cast<IRExpr>(op));
}
// A = B IRBinaryOp C
else if (auto binary_instr = bin_op_ir(instr))
{
irstmnt_t result = binary_instr->get_result();
irstmnt_t op1 = binary_instr->get_op1();
irstmnt_t op2 = binary_instr->get_op2();
if (auto reg = register_ir(op1))
op1 = get_top_or_create(reg, p);
if (auto reg = register_ir(op2))
op2 = get_top_or_create(reg, p);
if (auto reg = register_ir(result))
result = create_new_ssa_reg(reg, p);
new_instr = std::make_shared<IRBinOp>(binary_instr->get_bin_op_type(), std::dynamic_pointer_cast<IRExpr>(result), std::dynamic_pointer_cast<IRExpr>(op1), std::dynamic_pointer_cast<IRExpr>(op2));
}
// A = LOAD(B[INDEX])
else if (auto load_instr = load_ir(instr))
{
irstmnt_t destination = load_instr->get_destination();
irstmnt_t source = load_instr->get_source();
irstmnt_t index = load_instr->get_index();
if (auto reg = register_ir(source))
source = get_top_or_create(reg, p);
if (auto reg = register_ir(index))
index = get_top_or_create(reg, p);
if (auto reg = register_ir(destination))
destination = create_new_ssa_reg(reg, p);
new_instr = std::make_shared<IRLoad>(std::dynamic_pointer_cast<IRExpr>(destination), std::dynamic_pointer_cast<IRExpr>(source), std::dynamic_pointer_cast<IRExpr>(index), load_instr->get_size());
}
// A = New Class
else if (auto new_ir_instr = new_ir(instr))
{
irstmnt_t result = new_ir_instr->get_result();
if (auto reg = register_ir(result))
result = create_new_ssa_reg(reg, p);
new_instr = std::make_shared<IRNew>(std::dynamic_pointer_cast<IRExpr>(result), new_ir_instr->get_source_class());
}
// ret <reg>
else if (auto ret_instr = ret_ir(instr))
{
irstmnt_t return_value = ret_instr->get_return_value();
if (auto reg = register_ir(return_value))
return_value = get_top_or_create(reg, p);
new_instr = std::make_shared<IRRet>(std::dynamic_pointer_cast<IRExpr>(return_value));
}
// call <callee>(arg1, arg2, arg3...)
else if (auto call_instr = call_ir(instr))
{
std::vector<irexpr_t> new_args;
auto args = call_instr->get_args();
irstmnt_t ret_val = call_instr->get_ret_val();
for (auto arg : args)
{
auto reg = std::dynamic_pointer_cast<IRReg>(arg);
new_args.push_back(get_top_or_create(reg, p));
}
new_instr = std::make_shared<IRCall>(call_instr->get_callee(), call_instr->get_call_type(), new_args);
// maybe a return void method
if (ret_val != nullptr)
{
if (auto reg = register_ir(ret_val))
{
ret_val = create_new_ssa_reg(reg, p);
std::dynamic_pointer_cast<IRCall>(new_instr)->set_ret_val(std::dynamic_pointer_cast<IRExpr>(ret_val));
}
}
}
// STORE(A) = B
else if (auto store_instr = store_ir(instr))
{
irstmnt_t destination = store_instr->get_destination();
irstmnt_t source = store_instr->get_source();
irstmnt_t index = store_instr->get_index();
if (auto reg = register_ir(source))
source = get_top_or_create(reg, p);
if (auto reg = register_ir(index))
index = get_top_or_create(reg, p);
if (auto reg = register_ir(destination))
destination = create_new_ssa_reg(reg, p);
new_instr = std::make_shared<IRStore>(std::dynamic_pointer_cast<IRExpr>(destination), std::dynamic_pointer_cast<IRExpr>(source), std::dynamic_pointer_cast<IRExpr>(index), store_instr->get_size());
}
// ZComp
else if (auto zcomp = zcomp_ir(instr))
{
irstmnt_t op = zcomp->get_reg();
if (auto reg = register_ir(op))
op = get_top_or_create(reg, p);
new_instr = std::make_shared<IRZComp>(zcomp->get_comparison(), zcomp->get_result(), std::dynamic_pointer_cast<IRExpr>(op));
}
// BComp
else if (auto bcomp = bcomp_ir(instr))
{
irstmnt_t op1 = bcomp->get_reg1();
irstmnt_t op2 = bcomp->get_reg2();
if (auto reg = register_ir(op1))
op1 = get_top_or_create(reg, p);
if (auto reg = register_ir(op2))
op2 = get_top_or_create(reg, p);
new_instr = std::make_shared<IRBComp>(bcomp->get_comparison(), bcomp->get_result(), std::dynamic_pointer_cast<IRExpr>(op1), std::dynamic_pointer_cast<IRExpr>(op2));
}
// Alloca
else if (auto alloca = alloca_ir(instr))
{
irstmnt_t result = alloca->get_result();
irstmnt_t size = alloca->get_size();
if (auto reg = register_ir(result))
result = get_top_or_create(reg, p);
if (auto reg = register_ir(size))
size = get_top_or_create(reg, p);
new_instr = std::make_shared<IRAlloca>(std::dynamic_pointer_cast<IRExpr>(result), alloca->get_source_type(), std::dynamic_pointer_cast<IRExpr>(size));
}
// Phi node (only the result)
if (auto phi_instr = phi_ir(instr))
{
irstmnt_t result = phi_instr->get_result();
if (auto reg = register_ir(result))
result = create_new_ssa_reg(reg, p);
new_instr = std::make_shared<IRPhi>();
auto aux = std::dynamic_pointer_cast<IRPhi>(new_instr);
aux->add_result(std::dynamic_pointer_cast<IRExpr>(result));
for (auto param : phi_instr->get_params())
{
aux->add_param(param.second, param.first);
}
// not necessary a phi where we do not have
// more than one parameter
if (aux->get_params().size() < 2)
return nullptr;
}
return new_instr;
}
optimizer
We end the analysis part with the module I wasn’t able to fully program, the optimizer. The optimizer idea was having something like the optimization passes from LLVM, but of course, this is one of the most complex parts from the framework (even older versions from LLVM used an old version of the optimizer, and that part of LLVM was rewritten for a better version). In MjolnIR it was much more simple, so for the moment there was defined a function for optimizing one instruction from the IR (an IRStmnt), and for optimizing a full block (An IRBlock from an IRGraph), and they were defined in the following way:
using one_stmnt_opt_t = std::optional<irstmnt_t> (*)(irstmnt_t &);
using one_block_opt_t = std::optional<irblock_t> (*)(irblock_t &, irgraph_t &);
The optimizer class contained a vector to store functions from both:
std::vector<one_stmnt_opt_t> single_statement_optimization;
std::vector<one_block_opt_t> single_block_optimization;
And methods to add them:
/**
* @brief Add a single line optimization to the vector of optimizations
*
* @param opt
*/
void add_single_stmnt_pass(one_stmnt_opt_t opt);
/**
* @brief Add a single block optimization to the vector of optimizations
*
* @param opt
*/
void add_single_block_pass(one_block_opt_t opt);
Finally, there was a method to run the optimization pipeline:
/**
* @brief Run all the selected optimizations.
*
* @param func
*/
void run_analysis(irgraph_t func);
First, the optimizations were run instruction by instruction through the single statement optimizers, and statements were updated accordingly in case there was an optimization. Secondly, the optimizations for blocks, as well, the blocks were updated accordingly. Finally, since the optimizer class contained the reaching definition, this reaching definition analysis was re-run after the optimizations.
At that moment, I wrote a few optimizations, and the user was able to retrieve a new default optimizer with those optimizations:
optimizer_t NewDefaultOptimizer()
{
auto optimizer = std::make_shared<Optimizer>();
// single statement optimizers
optimizer->add_single_stmnt_pass(KUNAI::MJOLNIR::constant_folding);
// single block optimizers
optimizer->add_single_block_pass(KUNAI::MJOLNIR::nop_removal);
optimizer->add_single_block_pass(KUNAI::MJOLNIR::expression_simplifier);
optimizer->add_single_block_pass(KUNAI::MJOLNIR::instruction_combining);
return optimizer;
}
Later in the links you will be able to see how the optimizations were written, but here you have an example of expression_simplifier which took a block of code, and then tried to simplify mathematical expressions:
std::optional<irblock_t> expression_simplifier(irblock_t &block, irgraph_t &graph)
{
auto &stmnts = block->get_statements();
std::vector<KUNAI::MJOLNIR::irstmnt_t> new_statements;
// The idea here is to create a new vector with new statements
// also we will apply this optimizations until no more modifications
// are applied, because we can apply simplification in cascase.
bool modified = true;
while (modified)
{
// create a new state
modified = false;
new_statements.clear();
// here analyze the instructions, and apply simplifications
for (size_t i = 0, stmnts_size = stmnts.size(); i < stmnts_size;)
{
// SimplifySubInst
// X - (X - Y) -> Y
if (bin_op_ir(stmnts[i]) && bin_op_ir(stmnts[i])->get_bin_op_type() == IRBinOp::SUB_OP_T && (stmnts_size - i) >= 2 &&
bin_op_ir(stmnts[i + 1]) && bin_op_ir(stmnts[i + 1])->get_bin_op_type() == IRBinOp::SUB_OP_T)
{
auto first_instr = bin_op_ir(stmnts[i]);
auto second_instr = bin_op_ir(stmnts[i + 1]);
if (first_instr->get_op1()->equals(first_instr->get_op2()) &&
second_instr->get_op1()->equals(first_instr->get_result()))
{
irassign_t assign_inst = std::make_shared<IRAssign>(second_instr->get_result(), second_instr->get_op2());
new_statements.push_back(assign_inst);
i += 2;
modified = true;
continue;
}
}
Another one, instruction_combining was also fun to write in order to simplify other mathematical instructions, combining operands:
std::optional<irblock_t> instruction_combining(irblock_t &block, irgraph_t &graph)
{
...
// (A | (B ^ C)) ^ ((A ^ C) ^ B)
// =============================
// (A & (B ^ C))
if (bin_op_ir(stmnts[i]) && bin_op_ir(stmnts[i])->get_bin_op_type() == IRBinOp::XOR_OP_T
&& (stmnts_size - i) >= 5
&& bin_op_ir(stmnts[i+1]) && bin_op_ir(stmnts[i+1])->get_bin_op_type() == IRBinOp::OR_OP_T
&& bin_op_ir(stmnts[i+2]) && bin_op_ir(stmnts[i+2])->get_bin_op_type() == IRBinOp::XOR_OP_T
&& bin_op_ir(stmnts[i+3]) && bin_op_ir(stmnts[i+3])->get_bin_op_type() == IRBinOp::XOR_OP_T
&& bin_op_ir(stmnts[i+4]) && bin_op_ir(stmnts[i+4])->get_bin_op_type() == IRBinOp::XOR_OP_T)
{
auto first_xor = bin_op_ir(stmnts[i]);
auto second_or = bin_op_ir(stmnts[i+1]);
auto third_xor = bin_op_ir(stmnts[i+2]);
auto fourth_xor = bin_op_ir(stmnts[i+3]);
auto fifth_xor = bin_op_ir(stmnts[i+4]);
auto B = first_xor->get_op1();
auto C = first_xor->get_op2();
auto A = second_or->get_op1();
if (
second_or->get_op2()->equals(first_xor->get_result())
&& third_xor->get_op1()->equals(A)
&& third_xor->get_op2()->equals(C)
&& fourth_xor->get_op1()->equals(third_xor->get_result())
&& fourth_xor->get_op2()->equals(B)
&& fifth_xor->get_op1()->equals(second_or->get_result())
&& fifth_xor->get_op2()->equals(fourth_xor->get_result())
)
{
auto new_temporal = graph->get_last_temporal() + 1;
graph->set_last_temporal(new_temporal);
std::string temp_name = "t" + new_temporal;
auto temp_reg = std::make_shared<IRTempReg>(new_temporal,temp_name, 4);
auto created_xor = std::make_shared<IRBinOp>(IRBinOp::XOR_OP_T, temp_reg, B,C);
auto created_and = std::make_shared<IRBinOp>(IRBinOp::AND_OP_T, fifth_xor->get_result(), temp_reg, A);
new_statements.push_back(created_xor);
new_statements.push_back(created_and);
i += 5;
modified = true;
continue;
}
}
// if the instruction has not been optimized,
// means it is not an interesting expression
// then push it and go ahead.
new_statements.push_back(stmnts[i]);
i++;
}
I agree that the method wasn’t good since you had to specifically match each operand with each side of the instruction. In future versions the idea was to improve the optimizer to allow better rules, but finally, the project changed.
MjolnIR - Dalvik Bytecode Lifting
We reach the last section, which covers the lifting process that I will try to summarize to make this last part of the blog simple.
The lifter was able to lift the disassembled instructions from Kunai, the lifter was able to lift one single instruction to add it to a block, a block to add it to an IRGraph, and the main method lift_android_method received two Kunai objects in order to provide a full lifted Method in an IRGraph object.
MJOLNIR::irgraph_t lift_android_method(DEX::MethodAnalysis* method_analysis, DEX::Analysis* android_analysis);
bool lift_android_basic_block(DEX::DVMBasicBlock* basic_block, MJOLNIR::irblock_t& bb);
bool lift_android_instruction(DEX::Instruction* instruction, MJOLNIR::irblock_t& bb);
The process of lifting was just going block by block, lifting it, and for each block, instruction by instruction. Once all the instructions were lifted, the control-flow was created between blocks. Jump analysis and a fallthrough analysis were done to correctly detect the targets from the jumps, but also to correctly detect the fallthrough blocks. This is the function used to lift each Android method:
MJOLNIR::irgraph_t LifterAndroid::lift_android_method(DEX::MethodAnalysis* method_analysis, DEX::Analysis* android_analysis)
{
auto & bbs = method_analysis->get_basic_blocks()->get_basic_blocks();
size_t n_bbs = bbs.size();
// set android_analysis
this->android_analysis = android_analysis;
// graph returnedd by
MJOLNIR::irgraph_t method_graph = std::make_shared<MJOLNIR::IRGraph>();
// first of all lift all the blocks
for (auto bb : bbs)
{
MJOLNIR::irblock_t lifted_bb = std::make_shared<MJOLNIR::IRBlock>();
this->lift_android_basic_block(bb.get(), lifted_bb);
lifted_blocks[bb.get()] = lifted_bb;
method_graph->add_node(lifted_bb);
}
// Create Control Flow Graph using the children nodes
// from the method blocks.
for (auto bb : bbs)
{
auto & next_bbs = bb->get_next();
auto current_bb = lifted_blocks[bb.get()];
for (auto next_bb : next_bbs)
{
auto block = std::get<2>(next_bb).get();
if (lifted_blocks.find(block) == lifted_blocks.end())
continue;
if (lifted_blocks[block]->get_number_of_statements() == 0)
continue;
auto last_instr = lifted_blocks[block]->get_statements().back();
// unsigned jumps are fixed later, they only have to point
// to where jump targets
if (last_instr->get_op_type() != MJOLNIR::IRStmnt::UJMP_OP_T)
method_graph->add_edge(current_bb, lifted_blocks[block]);
}
}
this->jump_target_analysis(bbs, method_graph);
optimizer->fallthrough_target_analysis(method_graph);
method_graph->set_last_temporal(temp_reg_id - 1);
// clean android_analysis
this->android_analysis = nullptr;
return method_graph;
}
The translation of every instruction means understanding the semantic of each instruction, and creating an IR instruction that fits that semantic. The lift_android_instruction function was a veeeery long function with a veeeery long switch statement that detected the opcode of the instruction, and depending on the opcode, the functionality of the instruction was emulated with an IR instruction. A very simple example, the move instruction:
case DEX::DVMTypes::Opcode::OP_MOVE:
case DEX::DVMTypes::Opcode::OP_MOVE_WIDE:
case DEX::DVMTypes::Opcode::OP_MOVE_OBJECT:
{
MJOLNIR::irstmnt_t assignment_instr;
auto instr = reinterpret_cast<DEX::Instruction12x*>(instruction);
auto dest = instr->get_destination();
auto src = instr->get_source();
auto dest_reg = make_android_register(dest);
auto src_reg = make_android_register(src);
assignment_instr = std::make_shared<MJOLNIR::IRAssign>(dest_reg, src_reg);
bb->append_statement_to_block(assignment_instr);
break;
}
The design of a very long switch wasn’t good at all I think, so in newer versions, this long switch was replaced by an unordered_map and function pointers, these functions created through a template, and from the template different functions were specialized depending on the opcode or the type of the instruction.
Together with the lifter for the instructions, I created different helper functions to create data types like registers, temporal registers, strings, classes, fields, etc:
MJOLNIR::irreg_t make_android_register(std::uint32_t reg_id);
MJOLNIR::irtempreg_t make_temporal_register();
MJOLNIR::irtype_t make_none_type();
MJOLNIR::irconstint_t make_int(std::uint64_t value, bool is_signed, size_t type_size);
MJOLNIR::irstring_t make_str(std::string value);
MJOLNIR::irclass_t make_class(DEX::Class* value);
MJOLNIR::irfundamental_t make_fundamental(DEX::Fundamental* value);
MJOLNIR::irfield_t make_field(DEX::FieldID* field);
Links
Next, I will paste the links of the code where you can read the whole sources for all I have talked about in the post.
- Headers
- IRGraph: https://github.com/Fare9/KUNAI-static-analyzer/blob/main/old/src/include/KUNAI/mjolnIR/ir_graph.hpp
- All the classes for defining the instructions of MjolnIR: https://github.com/Fare9/KUNAI-static-analyzer/blob/main/old/src/include/KUNAI/mjolnIR/ir_grammar.hpp
- All the analysis classes, the graph analyses, the optimizer, reaching definition, etc: https://github.com/Fare9/KUNAI-static-analyzer/tree/main/old/src/include/KUNAI/mjolnIR/Analysis
- The definitions from the lifter: https://github.com/Fare9/KUNAI-static-analyzer/blob/main/old/src/include/KUNAI/mjolnIR/Lifters/lifter_android.hpp
- Sources
- Code from
IRBlocks: https://github.com/Fare9/KUNAI-static-analyzer/blob/main/old/src/mjolnIR/ir_blocks.cpp - Code from
IRExprs: https://github.com/Fare9/KUNAI-static-analyzer/blob/main/old/src/mjolnIR/ir_expr.cpp - Code from
IRGraph: https://github.com/Fare9/KUNAI-static-analyzer/blob/main/old/src/mjolnIR/ir_graph.cpp - Code from
IRStmnts: https://github.com/Fare9/KUNAI-static-analyzer/blob/main/old/src/mjolnIR/ir_stmnt.cpp - Code from
IRTypes: https://github.com/Fare9/KUNAI-static-analyzer/blob/main/old/src/mjolnIR/ir_type.cpp - Some utilities to work with the IR: https://github.com/Fare9/KUNAI-static-analyzer/blob/main/old/src/mjolnIR/ir_utils.cpp
- All the analysis code: https://github.com/Fare9/KUNAI-static-analyzer/tree/main/old/src/mjolnIR/Analysis
- The code from the lifter: https://github.com/Fare9/KUNAI-static-analyzer/blob/main/old/src/mjolnIR/Lifters/lifter_android.cpp
- Code from
Last Words
So… Here we are my old friend… This is the end of this long post. And maybe you jumped here directly from the beginning… But I really hope this post was useful for you, or for your team, or for your PhD thesis, master thesis or even undergrad thesis.
I wrote Kunai, mostly by my own, with learning purposes, even if the code grew enough to become part of my PhD thesis, but I was just chasing knowledge. I was able to improve my knowledge about the Android Dalvik file format, in programming with C++, in writing static binary analysis tools… I learned a lot. And this knowledge was pretty useful to get my current job. And now I wanted to give this knowledge to everyone else.
I think here is the place where I can say thank you to some people, so… Special thanks to Rob who has helped me a lot during my beginnings in Quarkslab, Matteo who always gave me his opinion about the implemented analyses, to Juan, Antonio, Angela (who also added her small contribution to the project), Qiqi (who was with me when I published this version of Kunai: Japanese version), to all my colleagues from Quarkslab, and my friends from Lega Kai. Probably I forget many other people, but specially thanks to you for reading until here.

