Solving the hack.lu 2021 OLLVM Challenge with Triton

In continuation of our previous post on employing Triton for tackling challenges through symbolic execution and SMT Solving, this time we will take on an obfuscated challenge. Specifically, we’ll delve into a challenge from hack.lu 2021, which has already been conquered by Jonathan Salwan. The binary for this challenge can be accessed through this link.
In this post, our focus will be on understanding how the binary operates. While we won’t delve deeply into the mathematics involved in the challenge, we will learn how to solve it using Z3. Additionally, we will explore techniques to refine the final expression, and I’ll even share code from a blog where the ultimate expression is reversed.
For those interested, the necessary tools for this endeavor can be found here: Triton and Ghidra.
Authors
- Eduardo Blazquez
The Challenge
As mentioned in the previous post, we are dealing with an ELF file designed for a 64-bit architecture. This file is dynamically linked, stripped, and has a size of 495KB. Extracting this essential information is straightforward using a couple of Linux commands:
$ file ollvm
ollvm: ELF 64-bit LSB executable, x86-64, version 1 (SYSV), dynamically linked, interpreter /lib64/ld-linux-x86-64.so.2, for GNU/Linux 3.2.0, stripped
$ ls -lah ollvm
-rwxrwx--- 1 symbolic symbolic 495K jul 15 17:23 ollvm
Once again, we are required to provide an argument to run the program. Alternatively, we can infer the necessary argument by executing the program without any input:
$ ./ollvm
Expected 1 parameters
Additionally, we discovered that this parameter must adhere to a specific format, as an input like -h to display help information does not function as intended.
$ ./ollvm -h
Argument -h cannot be converted, exiting
As a last test, I will test the program with a couple of numbers and showcase the corresponding outputs. It turns out that when we provide numerical inputs, the program generates specific output values. Let’s examine the outputs in the following code snippet:
$ ./ollvm 1
Output: 9a1e0411b56b3264
$ ./ollvm 2
Output: 8c1225f9a1f83264
$ ./ollvm 0x20
Output: 88af74eef5623264
$ ./ollvm 0b1100
Output: 953a4f4e4e823264
The only thing I’m doing is providing the program with a number in different formats (decimal, hexadecimal, and binary). As I observe, the program always returns an output of the same size, but each input number produces a different output. I suspect that the program uses some kind of hash function for each provided number.
This mathematical function can accept inputs of any size and, in theory, provides an output of a fixed size that varies for each unique input. Even a slight modification in the input can result in a significant change in the output.
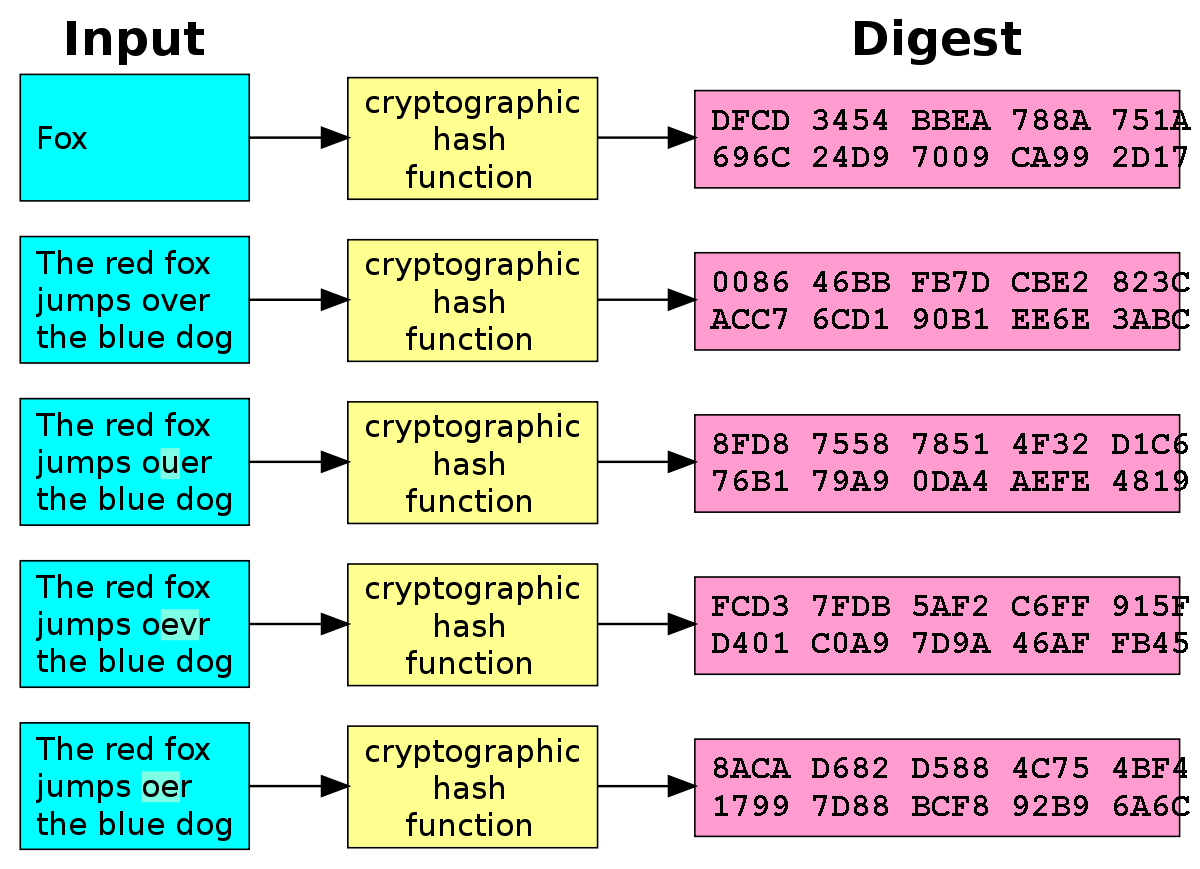
Let’s explore the binary directly on Ghidra’s disassembler in order to discover how the binary works, and how we can proceed with the analysis for solving the challenge with Triton.
Analyzing the Challenge with Ghidra (and a little of GDB)
In the previous post, I explained the process of analyzing a binary using Ghidra. To begin, we create a Ghidra project, import the binary into the working area (just pressing i), and then open it with CodeBrowser. Subsequently, we instruct Ghidra to analyze the binary.
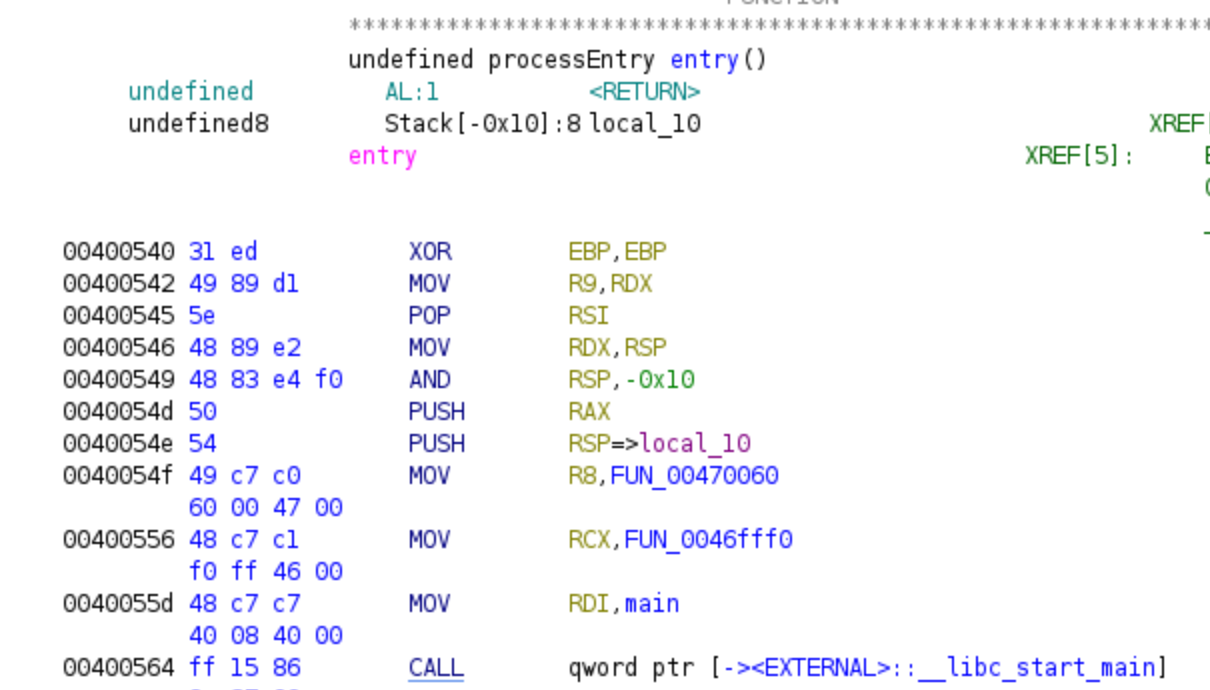
On the main disassembly screen, we can observe the disassembled code starting from the entry function, as indicated by the ELF header. As a reminder from the previous post, this function calls the __libc_start_main function from the libc library, with its first parameter stored in the RDI register—a pointer to the main function written by the developer. Therefore, in the next picture, the first parameter has already been renamed for clarity.
Next, I can directly navigate to the main function and format it to show the return type int, along with the parameters (int argc, char **argv). This formatting will provide us with a clearer view in the decompiler:
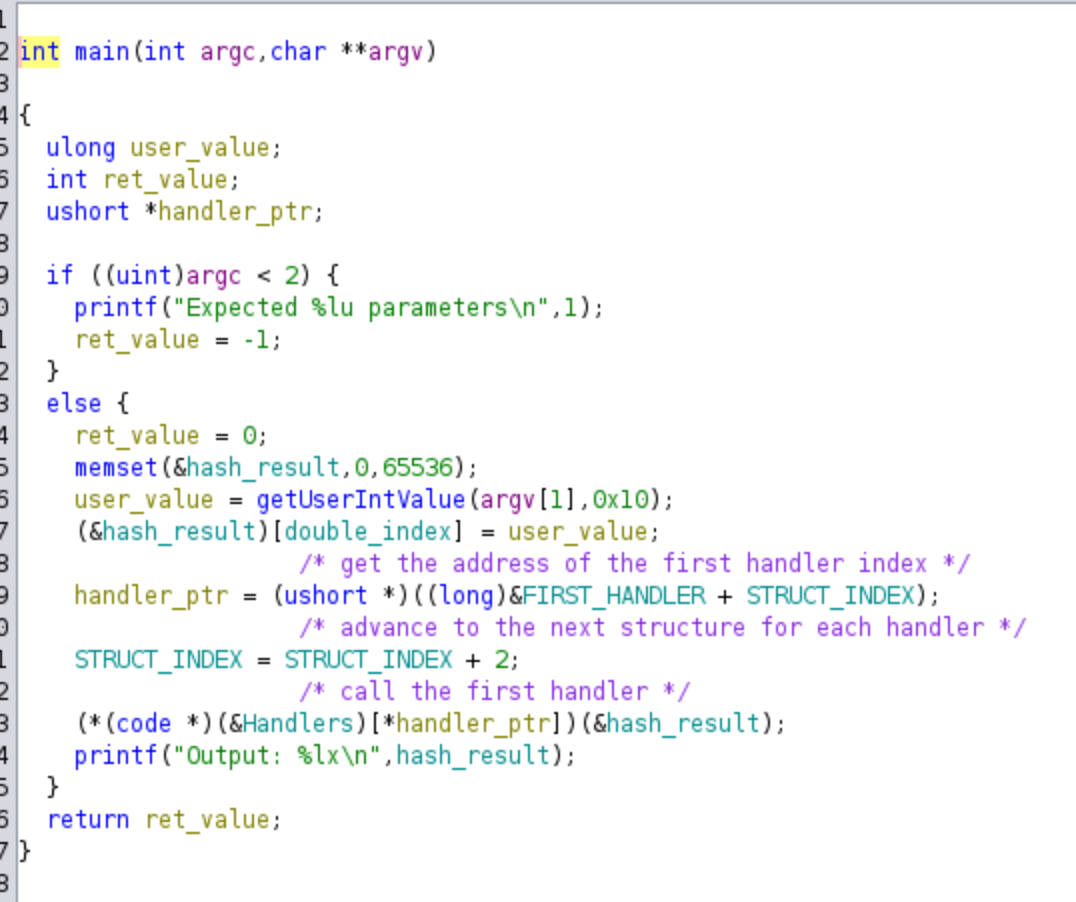
The first part of the code checks the argc value; if it’s equal to or greater than 2, we receive an error message indicating that only 1 parameter is expected. On the other hand, when a single parameter (a buffer of 64K) is provided, I’ve renamed it as hash_results, and it is set to 0. The code then calls a function, which I’ve renamed as getUserIntValue, passing argv[1] and the value 0x10 as parameters. The output from this function is stored in index 0x03 of the hash_results buffer, and I will show it in the next code snippet:
00400899 8b 0d c1 MOV ECX,dword ptr [double_index] = 00000003h
a7 27 00
0040089f 48 89 04 MOV qword ptr [0x67b280 + RCX*0x8]=>user_value_storage,user_va = ??
cd 80 b2
67 00
Where double_index is equals to 0x3 and the value 0x67b280 is the hash_results buffer.
Finally, we encounter a somewhat unusual piece of code, where a value is retrieved, the pointer is advanced by 2, and then a function is indirectly called using the retrieved value as an index in an array of pointers, which I’ll refer to as handlers. To obtain the address of the handler, we simply retrieve the value of handler_ptr, multiply it by 8, and add it to the base address 0x0067a050, where the handler pointers are located:
(0x1C9 * 8) + 0x0067a050 = 0x67ae98
# Pointerd memory
0067ae98 b0 36 46 addr FUN_004636b0
00 00 00
00 00
The first called handler is the function FUN_004636b0. We can be certain of this by using gdb, and in my case, I will utilize gdb-gef, which provides a better code view within the debugger. The call function resides at address 0x004008cc. To set a breakpoint in gdb, use the command b *0x004008cc, and then execute the program with any input:
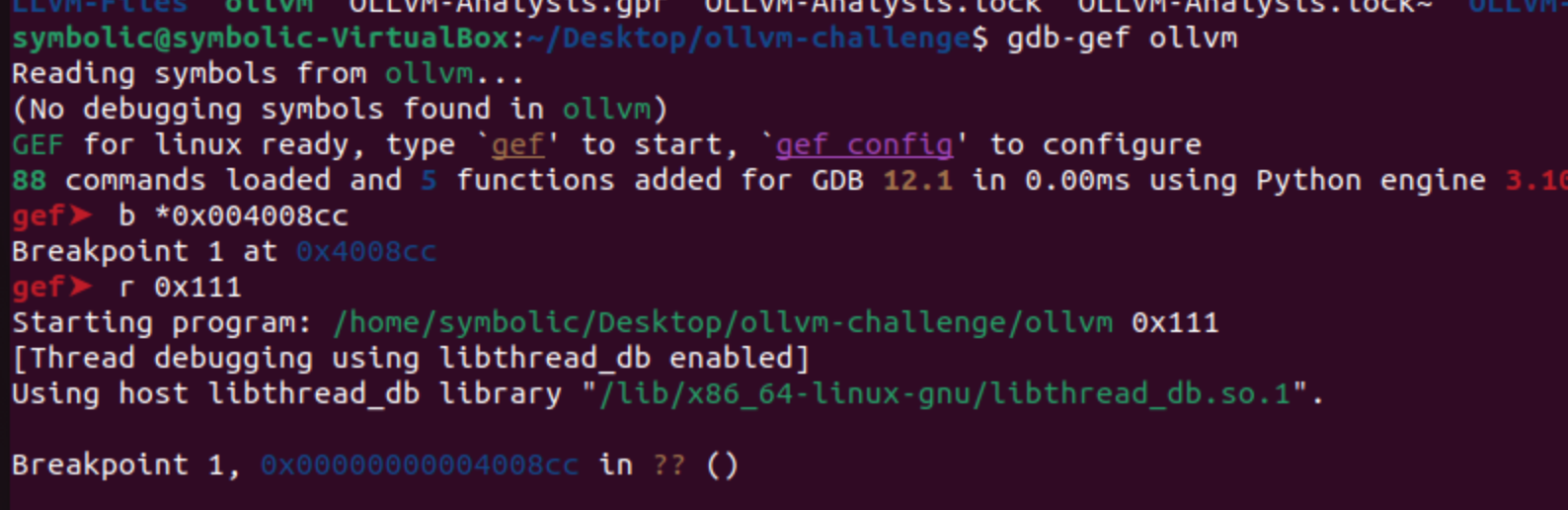
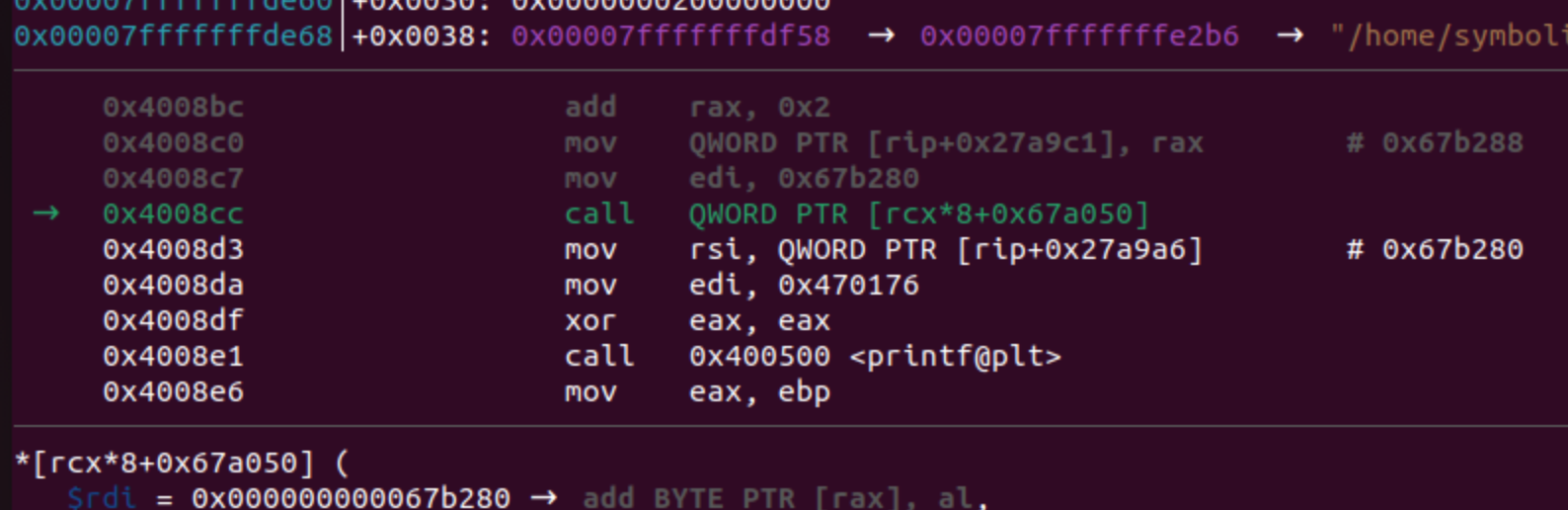
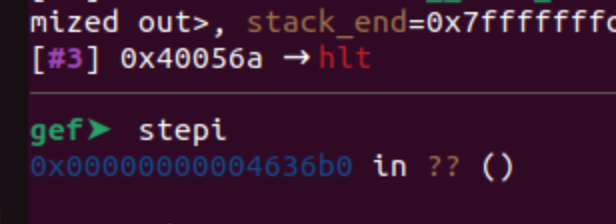
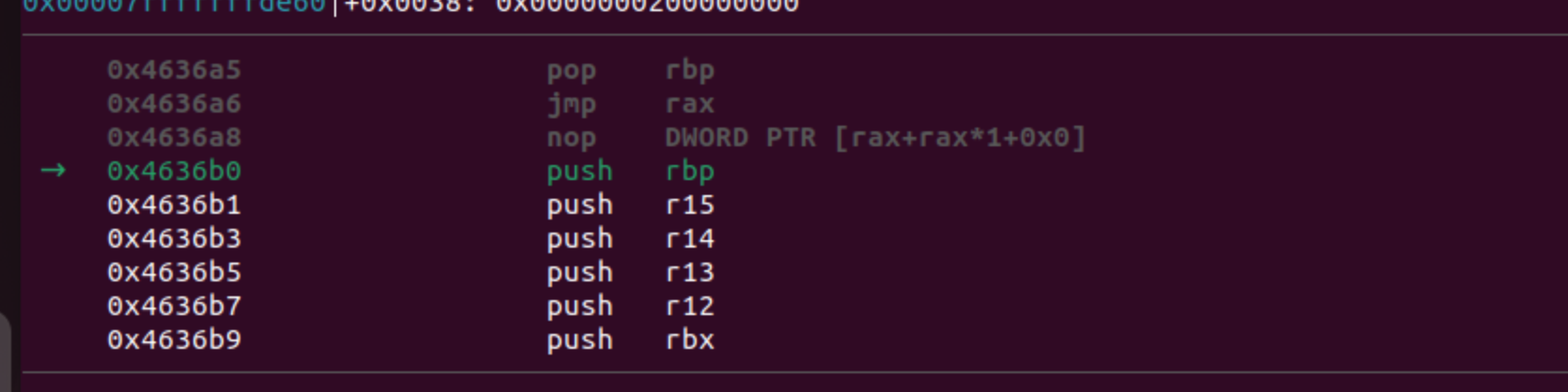
In all the previous images, I demonstrated the process of obtaining the same address we obtained statically, but this time using the debugger. Later on, I will illustrate how we can achieve these values using Triton.
An essential point to note from the main function is that an index value is advanced by 2, as I mentioned earlier. This is interesting because the protection employs a structure containing various useful values for hash calculation and storing the resulting hash on each handler. However, before delving into that, let’s first take a closer look at the code for the initial handler. The code is obfuscated, and the resulting mathematical expression (which I’ll show with Triton later) will also be challenging to comprehend:
void FirstHandler(void)
{
...
const1 = *(long *)((long)&FIRST_HANDLER.const1 + STRUCT_INDEX);
const2 = *(ulong *)((long)&FIRST_HANDLER.const2 + STRUCT_INDEX);
hash_value1 = (&hash_result)[*(ushort *)((long)&FIRST_HANDLER.hash1 + STRUCT_INDEX)];
hash_value2 = (&hash_result)[*(ushort *)((long)&FIRST_HANDLER.hash2 + STRUCT_INDEX)];
auVar2._8_8_ = 0;
auVar2._0_8_ = const2 & 0xffffffff;
uVar18 = SUB168((ZEXT816(0) << 0x40 | ZEXT816(0x11a9b37518b9d587)) % auVar2,0);
bVar9 = (byte)hash_value2 & 0x3f;
lVar19 = hash_value2 + const1;
if (const2 != 0) {
bVar9 = 0;
lVar19 = 0;
}
bVar10 = const1 == 0 || const2 == 0;
uVar25 = (uint)bVar10;
auVar3._8_8_ = 0;
auVar3._0_8_ = const2 & 0xffffffff;
auVar3 = (ZEXT816(0) << 0x40 | ZEXT816(0x17e87cc7bd2f0913)) % auVar3;
lVar20 = auVar3._0_8_;
uVar1 = lVar20 - 1;
uVar11 = auVar3._0_4_;
uVar26 = (ulong)(((int)uVar1 * 2 ^ 0xfffffffdU) & uVar11) | 2;
uVar23 = 1 - uVar26 ^ lVar20 + 0x7fffffffffffffffU;
auVar4._8_8_ = 0;
auVar4._0_8_ = (const2 | 0xffffffff00000000) + 0x100000000;
uVar5 = (long)uVar23 >> 0x3f;
uVar14 = -uVar5;
uVar22 = ((~(-(int)const1 | ~uVar25) | uVar25) & uVar25) * const2 + hash_value1;
iVar12 = (uint)(byte)(const2 >> 0x38) * 0x41225f1;
uVar16 = const2 >> 0x20 & 0xff;
uVar25 = (uint)uVar16;
uVar13 = (iVar12 - (uVar25 * uVar25 & 2 ^ uVar25)) * (iVar12 - uVar25);
uVar25 = uVar13 + 0xfe;
uVar8 = (const2 & 0xffffffff) >> 0x18;
uVar29 = (uint)((const2 & 0xffffffff) >> 0x18);
uVar6 = -((ulong)(~(uint)(const2 >> 0x20) & uVar29 & uVar13 ^ ((uVar25 | 2) & uVar25) + 2 & uVar29
) * (-hash_value1 - const1));
uVar34 = const2 >> 0x10 & 0xffff;
uVar32 = const2 >> 0x20 & 0xffff;
uVar7 = const2;
if (hash_value1 == 0) {
uVar7 = 0;
}
uVar15 = 0;
if (bVar10) {
uVar15 = const2;
}
uVar21 = (const2 >> 0x38) - 0xf6 & 0xf4 - (const2 >> 0x38);
uVar28 = const2 & 0xff;
uVar31 = const2 >> 0x10 & 0xff;
uVar30 = 0x86 - uVar31 & uVar31 - 0x88;
uVar27 = uVar16 - 0x5c & 0x5a - uVar16 & uVar8 - 0x83 & 0x81 - uVar8;
uVar8 = const2 >> 0x28 & 0xff;
uVar16 = uVar8 - 0x14 & 0x12 - uVar8;
uVar8 = const2 >> 0x30 & 0xff;
uVar8 = uVar8 - 0xac & 0xaa - uVar8;
uVar35 = ~(-(ulong)((uint)(2L << ((byte)(uVar28 - 0x44) & 0x3f)) & 1) | uVar28 - 0x44) &
uVar28 - 0x45;
uVar24 = const2 >> 8 & 0xff;
uVar17 = uVar16 & uVar8 & uVar27;
uVar33 = uVar24 - 0x3b & 0x39 - uVar24;
uVar28 = 0x43 - uVar28 & uVar28 - 0x45 & uVar33;
lVar20 = -((long)(uVar8 & uVar30 & uVar28 & uVar31 + 0x7fffffffffffff79 & uVar16 & uVar27) >> 0x3f
);
uVar25 = (uint)(uVar17 >> 0x20) & (uint)(uVar30 >> 0x20);
uVar16 = (ulong)(((uint)(uVar28 >> 0x20) & uVar25) >> 0x1f);
uVar8 = (lVar20 - ((long)(uVar33 & uVar30 & uVar17 & uVar35 & uVar21) >> 0x3f)) - uVar16;
(&hash_result)[*(ushort *)((long)&FIRST_HANDLER.result_hash + STRUCT_INDEX)] =
(((((long)(-3 - ((uVar18 | 0xfffffffffffffffe) & ~(uVar18 + 1 & (uVar18 | 0x1fffffffe)))) >>
0x3f & hash_value2 << bVar9) + lVar20 + 1) - uVar16) -
(ulong)((((uint)(uVar24 - 0x3a >> 0x20) | (uint)(uVar24 - 0x3b >> 0x20)) &
(uint)(0x39 - uVar24 >> 0x20) & (uint)(uVar35 >> 0x20) & uVar25) >> 0x1f) *
((long)uVar21 >> 0x3f)) + ~uVar8 + (const1 * const2 & const2) * uVar8 +
((((uVar15 + hash_value1) - uVar22) + uVar14 | uVar14) * uVar22 +
((long)(uVar32 - 0x2163 & 0x2161 - uVar32 &
(const2 & 0xffff) - 0xa2e7 & 0xa2e5 - (const2 & 0xffff) & (const2 >> 0x30) - 0xe63 &
uVar34 - 0x7fdf & 0x7fdd - uVar34 &
0xe61 - (ulong)((~(uint)(2L << ((byte)(const2 >> 0x30) & 0x3f)) | 0xfffffffd) &
(uint)(ushort)(const2 >> 0x30))) >> 0x3f & uVar7 + lVar19) +
((uVar6 ^ 2 | uVar6) & uVar6) ^
-(uVar5 & uVar22 &
~(-((long)((uVar26 - ((ulong)((SUB164((ZEXT816(0) << 0x40 | ZEXT816(0x17e87cc7bd2f0913)) %
auVar4,0) * 2 - 2U ^ 0xfffffffd) & uVar11) | 2)) - 1 &
uVar1 | uVar23) >> 0x3f) * uVar22)));
next_handler_index = (short *)((long)&FIRST_HANDLER.next_handler + STRUCT_INDEX);
STRUCT_INDEX = STRUCT_INDEX + 24;
(*(code *)(&Handlers)[*next_handler_index])(&hash_result);
return;
}
As observed, the expression employs various constants alongside arithmetic and boolean expressions, collectively referred to as Mixed Boolean-Arithmetic (MBA) expressions. These expressions are particularly effective for obfuscating mathematical expressions that would otherwise be much simpler. For further understanding, I recommend exploring theses such as Obfuscation with Mixed Boolean-Arithmetic Expressions: reconstruction, analysis, and simplification tools by Ninon Eyrolles or Analysis and applications of orthogonal approaches to simplify Mixed Boolean-Arithmetic expressions by Arnau Gamez.
Since the expressions will be solved using Z3, I will focus on other aspects of the obfuscation. As evident here, the call is an indirect call to the list of handlers, which entirely disrupts the call graph.
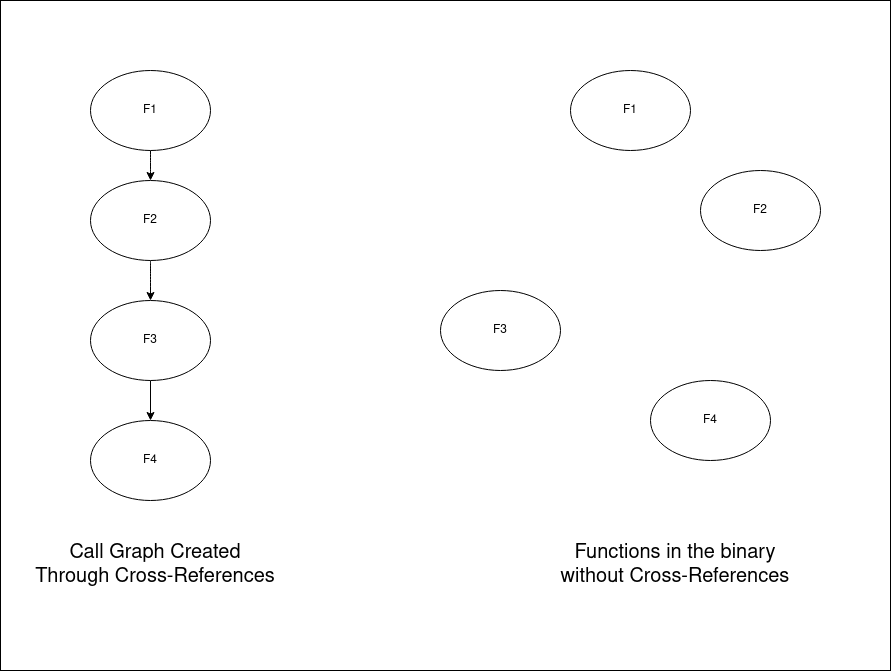
As I previously said, we observed that a pointer was advanced 2 bytes, and in different parts of the code we observe access to an structure:
const1 = *(long *)((long)&FIRST_HANDLER.const1 + STRUCT_INDEX);
const2 = *(ulong *)((long)&FIRST_HANDLER.const2 + STRUCT_INDEX);
hash_value1 = (&hash_result)[*(ushort *)((long)&FIRST_HANDLER.hash1 + STRUCT_INDEX)];
hash_value2 = (&hash_result)[*(ushort *)((long)&FIRST_HANDLER.hash2 + STRUCT_INDEX)];
(&hash_result)[*(ushort *)((long)&FIRST_HANDLER.result_hash + STRUCT_INDEX)] =
(((((long)(-3 - ((uVar18 | 0xfffffffffffffffe) & ~(uVar18 + 1 & (uVar18 | 0x1fffffffe)))) >>
0x3f & hash_value2 << bVar9) + lVar20 + 1) - uVar16) -
(ulong)((((uint)(uVar24 - 0x3a >> 0x20) | (uint)(uVar24 - 0x3b >> 0x20)) &
(uint)(0x39 - uVar24 >> 0x20) & (uint)(uVar35 >> 0x20) & uVar25) >> 0x1f) *
((long)uVar21 >> 0x3f)) + ~uVar8 + (const1 * const2 & const2) * uVar8 +
((((uVar15 + hash_value1) - uVar22) + uVar14 | uVar14) * uVar22 +
((long)(uVar32 - 0x2163 & 0x2161 - uVar32 &
(const2 & 0xffff) - 0xa2e7 & 0xa2e5 - (const2 & 0xffff) & (const2 >> 0x30) - 0xe63 &
uVar34 - 0x7fdf & 0x7fdd - uVar34 &
0xe61 - (ulong)((~(uint)(2L << ((byte)(const2 >> 0x30) & 0x3f)) | 0xfffffffd) &
(uint)(ushort)(const2 >> 0x30))) >> 0x3f & uVar7 + lVar19) +
((uVar6 ^ 2 | uVar6) & uVar6) ^
-(uVar5 & uVar22 &
~(-((long)((uVar26 - ((ulong)((SUB164((ZEXT816(0) << 0x40 | ZEXT816(0x17e87cc7bd2f0913)) %
auVar4,0) * 2 - 2U ^ 0xfffffffd) & uVar11) | 2)) - 1 &
uVar1 | uVar23) >> 0x3f) * uVar22)));
next_handler_index = (short *)((long)&FIRST_HANDLER.next_handler + STRUCT_INDEX);
STRUCT_INDEX = STRUCT_INDEX + 24;
(*(code *)(&Handlers)[*next_handler_index])(&hash_result);
Each part of the code accesses a specific portion of the structure. Initially, two constants of 8 bytes each are accessed and stored in local variables. Next, two hash values from the hash_result table are retrieved using indices from the structure. Once the final hash is calculated, it is stored in the index pointed to by the result_hash value within the structure. Finally, towards the end of the code, there is access to another field that points to the next handler to be executed.
To create the structure in Ghidra, follow these steps. First, navigate to the data type manager located at the bottom-left corner of the CodeBrowser:
We will right click in the name of our file (in this case ollvm), and we will see the next options:
We just choose to create a new->structure and we will see a screen like the next:
While I won’t provide a detailed explanation of how I obtained each part of the structure, I will highlight some aspects of the code that will aid in understanding how it’s possible to extract each field from the structure:
assume RDX = 0x2
004636ba 48 8b 15 MOV RDX,qword ptr [STRUCT_INDEX] = ??
c7 7b 21 00
004636c1 0f b7 82 MOVZX EAX,word ptr [RDX + FIRST_HANDLER]
64 b0 67 00
004636c8 48 89 44 MOV qword ptr [RSP + first_value],RAX
24 f0
004636cd 0f b7 82 MOVZX EAX,word ptr [RDX + HANDLER_STRUCTURE]
66 b0 67 00
004636d4 0f b7 8a MOVZX ECX,word ptr [RDX + CONST1]
68 b0 67 00
004636db 48 8b ba MOV RDI,qword ptr [RDX + QWORD_CONST1]
6a b0 67 00
004636e2 48 89 54 MOV qword ptr [RSP + first_constant],RDX
24 f8
004636e7 48 8b 9a MOV RBX,qword ptr [RDX + QWORD_CONST2]
72 b0 67 00
004636ee 4c 8b 3c MOV R15,qword ptr [hash_result + RAX*0x8] = ??
c5 80 b2
67 00
004636f6 48 8b 34 MOV RSI,qword ptr [hash_result + RCX*0x8] = ??
cd 80 b2
67 00
If we recall from the main function, STRUCT_INDEX was set to 2. Next, we need to access the FIRST_HANDLER memory, add 2 to the address, and inspect the memory values using the debugger. Let’s observe the accessed values:
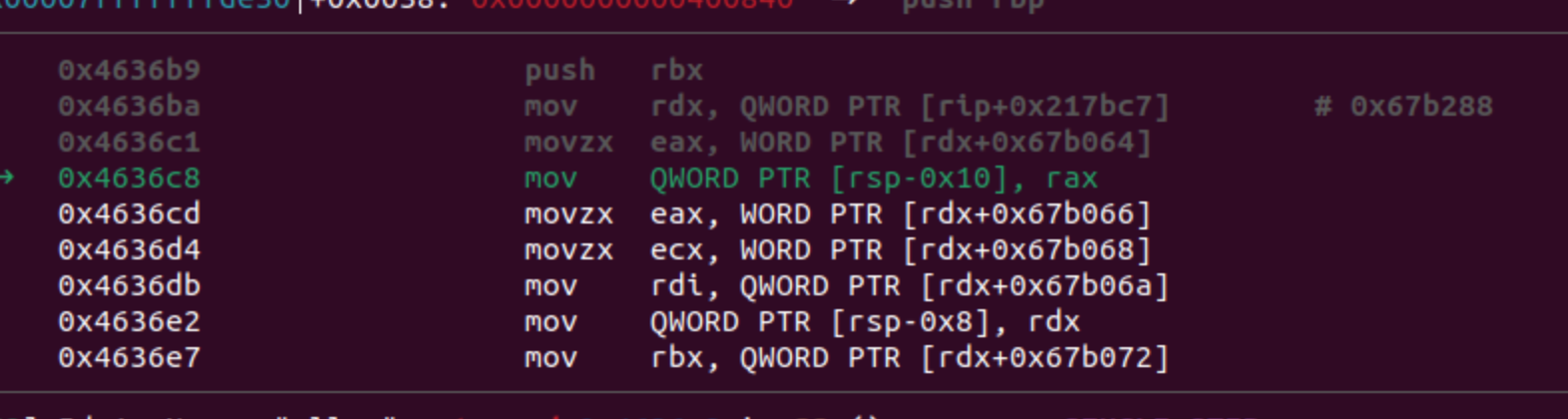
The values obtained are 0x2 and 0x3 for the hash index, and 0x4ddb14ee5c8771c5 and 0x56426f353ff403c2 for the constants. By searching for these results in the memory, we can locate the beginning of the structure. Additionally, there are two more values: result_hash with the value 0x2 and the value 0x1ea, which represents the index to the next handler. When we combine all these fields and assign a name, we define the next structure:
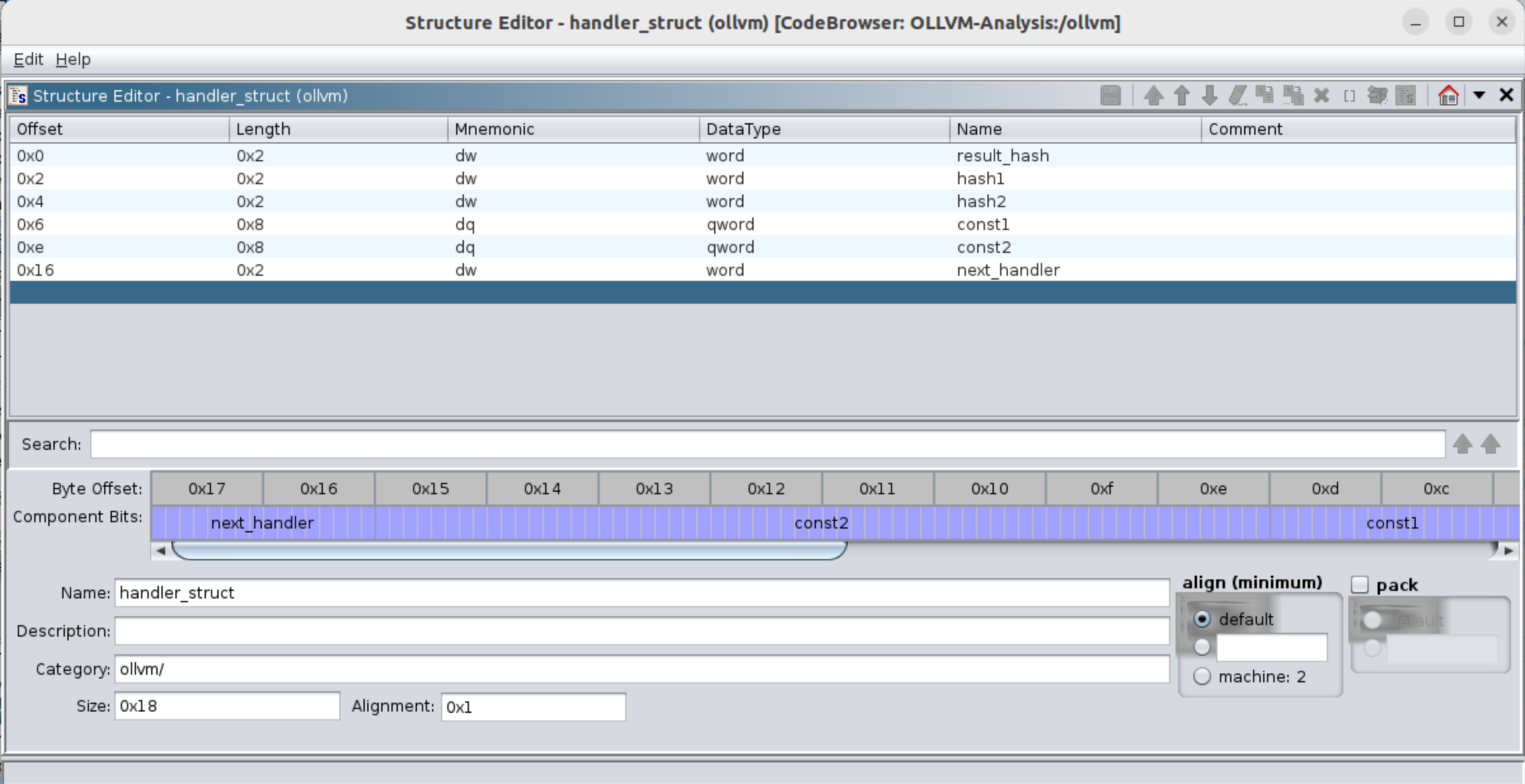
In C the structure would be the next:
struct handler_struct {
word result_hash;
word hash1;
word hash2;
qword const1;
qword const2;
word next_handler;
};
Each time the program completes a handler, it updates the STRUCT_INDEX value by adding 24 bytes, which precisely matches the size of this structure. As a result, we have a chain of structures, with one for each handler, to store values and point to the next handler. Let’s visualize this chain:
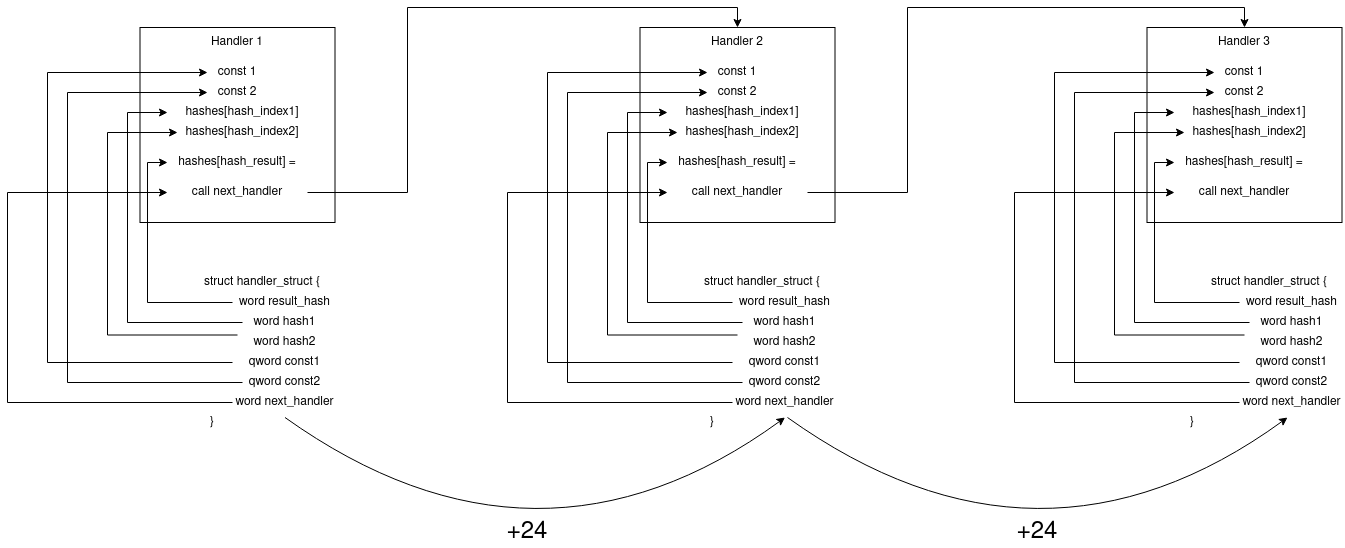
Following the process we followed before, we can calculate the next handlers, we can make use of the previous structure:
(0x1ea * 0x8) + 0x0067a050 = 0x0067afa0
0067afa0 f0 b1 46 addr FUN_0046b1f0
00 00 00
00 00
(0x49 * 0x8) + 0x0067a050 = 0x0067a298
0067a298 60 fa 40 addr FUN_0040fa60
00 00 00
00 00
...
But we will extract this data using Triton for each one of the handlers the program executes.
Analyzing the binary with Triton
As a reminder from the previous post, when using Triton, we needed to perform several steps before emulating the binary. Firstly, we had to read the file, load it into memory following the sections from the ELF Binary, and apply some relocations before we could begin working with the binary. We achieved this using the Lief library. As we did in the previous post, the following code demonstrates these steps:
from triton import *
import string
import time
import lief
# Target binary
TARGET = "./ollvm"
# Global settings
SYMBOLIC = True
CONCRETE = not SYMBOLIC
# Memory mapping
BASE_PLT = 0x10000000
BASE_ARGV = 0x20000000
BASE_STACK = 0x9ffffff0
ERRNO = 0xa0000000
...
def loadBinary(triton_ctx, lief_binary):
'''
Use Lief parser in order to retrieve
information of the binary, and load it
in Triton's memory.
:param triton_ctx: context where triton stores all the information.
:param lief_binary: parser of lief with information about the headers.
'''
phdrs = lief_binary.segments
for phdr in phdrs:
size = phdr.physical_size
vaddr = phdr.virtual_address
print("[+] Loading 0x%06x - 0x%06x" % (vaddr, vaddr+size))
triton_ctx.setConcreteMemoryAreaValue(vaddr, list(phdr.content))
return
def makeRelocation(ctx, binary):
'''
Extract the addresses from the PLT, these will be used
to retrieve the addressed and hook the functions once we have to run them.
:param ctx: triton context for the emulation.
:param binary: lief binary parser.
'''
# Setup plt
print("[+] Applying relocations and extracting the addresses for the external functions")
for pltIndex in range(len(customRelocation)):
customRelocation[pltIndex][2] = BASE_PLT + pltIndex
relocations = [x for x in binary.pltgot_relocations]
relocations.extend([x for x in binary.dynamic_relocations])
# Perform our own relocations
for rel in relocations:
symbolName = rel.symbol.name
symbolRelo = rel.address
for crel in customRelocation:
if symbolName == crel[0]:
print('[+] Init PLT for: %s' % (symbolName))
ctx.setConcreteMemoryValue(MemoryAccess(
symbolRelo, CPUSIZE.QWORD), crel[2])
break
return
Furthermore, we require a hooking handler that will execute each emulated API and apply symbolization of the return register if a value is provided:
def hookingHandler(ctx):
'''
In case one of the run address is one from
the emulated functions, just call it and
get the result, check if it's needed to symbolize
the output register.
:param ctx: Triton's context for emulation.
'''
pc = ctx.getConcreteRegisterValue(ctx.registers.rip)
for rel in customRelocation:
if rel[2] == pc:
# Emulate the routine and the return value
state, ret_value = rel[1](ctx)
if ret_value is not None:
ctx.setConcreteRegisterValue(ctx.registers.rax, ret_value)
if state is SYMBOLIC:
print(f'[+] Symbolizing the return value')
ctx.symbolizeRegister(ctx.registers.rax)
# Get the return address
ret_addr = ctx.getConcreteMemoryValue(MemoryAccess(
ctx.getConcreteRegisterValue(ctx.registers.rsp), CPUSIZE.QWORD))
# Hijack RIP to skip the call
ctx.setConcreteRegisterValue(ctx.registers.rip, ret_addr)
# Restore RSP (simulate the ret)
ctx.setConcreteRegisterValue(ctx.registers.rsp, ctx.getConcreteRegisterValue(
ctx.registers.rsp)+CPUSIZE.QWORD)
return
In this instance, I have implemented two functions: pre_execution and post_execution, which will be invoked from the emulate function—right before and right after the call to processing from the TritonContext object. These functions include several parameters that prove useful for the analysis:
def pre_execution(ctx):
'''
Code to call before processing an instruction
'''
pc = ctx.getConcreteRegisterValue(ctx.registers.rip)
return pc
def post_execution(previous_pc, instruction, ctx):
'''
Code to call after processing an instruction
'''
pass
def emulate(ctx, pc):
'''
Emulation function, go over each instruction applying all the
symbolic execution to registers and memory.
:param ctx: Triton context to apply symbolic execution.
:param pc: the program counter value where to start and continue.
:valut_to_check: value to check once we wants to stop the execution.
'''
# emulation loop
while pc:
# print("[-] Running instruction at address: 0x%08X" % (pc))
opcodes = ctx.getConcreteMemoryAreaValue(pc, 16)
instruction = Instruction(pc, opcodes)
# if we want to bypass code, do it
# in this function
pc = pre_execution(ctx)
# process the instruction
ret = ctx.processing(instruction)
# if HALT, finish the execution
if instruction.getType() == OPCODE.X86.HLT:
break
# all the code after processing, goes here
post_execution(pc, instruction, ctx)
# apply one of the handlers that are not provided by
# Triton
hookingHandler(ctx)
# Next
pc = ctx.getConcreteRegisterValue(ctx.registers.rip)
With this structure in place, we have the ability to modify the instruction flow, allowing us to run our analysis immediately after the processing of each instruction. In the case of this binary, our primary focus will be on the post_execution function.
First of all, the hooks
Given that there are several API functions in this binary, we need to provide handlers for them. The most critical function is the one called at the start of the binary, __libc_start_main. Additionally, we have other functions such as memset, __errno_location, strtoul, and printf. For the first function, we will write the arguments to the program, while for the others, we will simply “emulate” their behavior. However, strtoul requires special attention as it receives our first argument and returns the unsigned long number version. This value serves as input for the hash function, and here we will symbolize the output of strtoul to ultimately obtain the expression required to solve the challenge. Below, you can find the code for these hooks:
def memset(ctx):
'''
Hook for memset set concrete memory value
'''
print('[+] memset hooked')
ptr = ctx.getConcreteRegisterValue(ctx.registers.rdi)
size = ctx.getConcreteRegisterValue(ctx.registers.rdx)
value = ctx.getConcreteRegisterValue(ctx.registers.rsi)
for i in range(size):
memset_mem_value = MemoryAccess(ptr+i, CPUSIZE.BYTE)
ctx.setConcreteMemoryValue(memset_mem_value, value)
return (CONCRETE, size)
def __errno_location(ctx):
'''
Return the address of ERRNO value
'''
print('[+] __errno_location hooked')
return (CONCRETE, ERRNO)
def strtoul(ctx):
'''
Hook for strtoul
'''
print('[+] strtoul hooked')
return (SYMBOLIC, int("0xdeadbeef", 16))
def libc_start_main(ctx):
'''
Emulation of libc start, here we will set the
arguments giving them an address in memory and
copying the values into that memory.
'''
print('[+] __libc_start_main hooked')
# Get arguments
main = ctx.getConcreteRegisterValue(ctx.registers.rdi)
# Push the return value to jump into the main() function
ctx.setConcreteRegisterValue(ctx.registers.rsp, ctx.getConcreteRegisterValue(
ctx.registers.rsp)-CPUSIZE.QWORD)
# set as return value the address of main
# avoid all the libc stuff
ret2main = MemoryAccess(ctx.getConcreteRegisterValue(
ctx.registers.rsp), CPUSIZE.QWORD)
ctx.setConcreteMemoryValue(ret2main, main)
# Setup argc / argv
ctx.concretizeRegister(ctx.registers.rdi)
ctx.concretizeRegister(ctx.registers.rsi)
# here write all the needed arguments
argvs = [
bytes(TARGET.encode('utf-8')), # argv[0]
b'1000000' + b'\00'
]
# Define argc / argv
base = BASE_ARGV
addrs = list()
# create the arguments
index = 0
for argv in argvs:
addrs.append(base)
ctx.setConcreteMemoryAreaValue(base, argv+b'\x00')
base += len(argv)+1
print('[+] argv[%d] = %s' % (index, argv))
index += 1
# set the pointer to the arguments
argc = len(argvs)
argv = base
for addr in addrs:
ctx.setConcreteMemoryValue(MemoryAccess(base, CPUSIZE.QWORD), addr)
base += CPUSIZE.QWORD
# finally set RDI and RSI values
ctx.setConcreteRegisterValue(ctx.registers.rdi, argc)
ctx.setConcreteRegisterValue(ctx.registers.rsi, argv)
return (CONCRETE, 0)
def printf(ctx):
'''
Hook for printf
'''
print("[+] printf Hooked")
output = ctx.getConcreteRegisterValue(ctx.registers.rsi)
print("Output: %lx" % (output))
return (CONCRETE, 0)
# this structure will be useful during emulation
# whenever the emulation jumps to any of the functions
# from the first field, use the second fields as hook.
customRelocation = [
['__libc_start_main', libc_start_main, None],
['memset', memset, None],
['__errno_location', __errno_location, None],
['strtoul', strtoul, None],
['printf', printf, None]
]
As evident from the previous snippet, symbolizing the return value is a straightforward process, as shown in the following code:
def strtoul(ctx):
'''
Hook for strtoul
'''
print('[+] strtoul hooked')
return (SYMBOLIC, int("0xdeadbeef", 16))
In the hookingHandler function, we will set the RAX register value as symbolic, and the returned value will be the concrete value from that register. In this case, the value will be 0xdeadbeef.
Retrieving the addresses of the handler
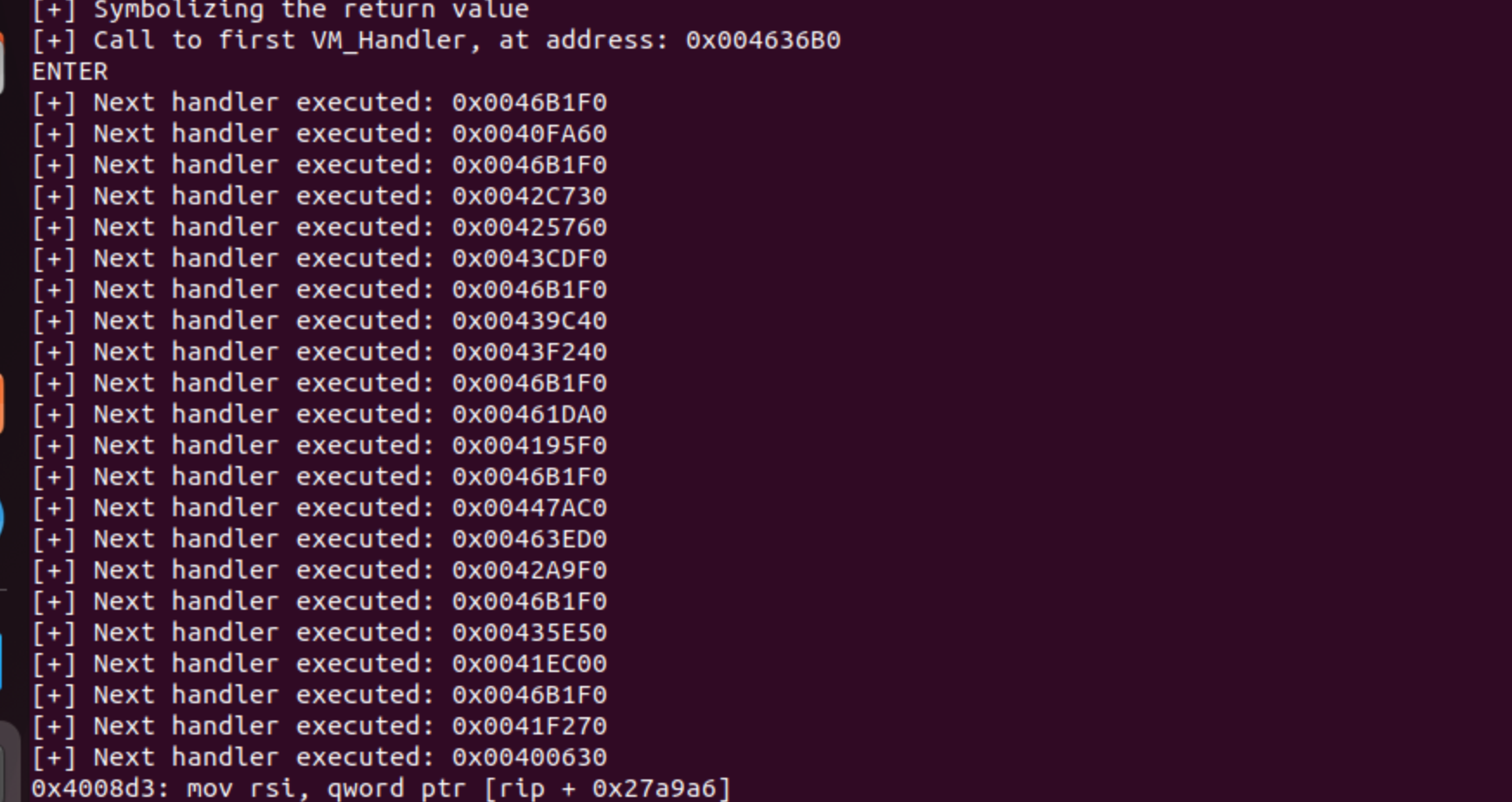
To retrieve the addresses of the handlers executed by the program, we have two approaches. As we previously saw, we can do this manually using the values from the structure or set breakpoints in a debugger. The first handler is executed using a call instruction, and the rest are executed directly with a jmp rax instruction. In the post_execution function, as mentioned earlier, I will write the code to extract the value for the call instruction, and for the jmp rax instruction, I will search for it dynamically during runtime.
def post_execution(previous_pc, instruction, ctx):
'''
Code to call after processing an instruction
'''
# to get the first handler
if previous_pc == 0x004008cc:
current_pc = ctx.getConcreteRegisterValue(ctx.registers.rip)
print("[+] Call to first VM_Handler, at address: 0x%08X" % (current_pc))
input("ENTER")
# check next handlers!
if "jmp rax" in str(instruction):
next_handler = ctx.getConcreteRegisterValue(ctx.registers.rax)
print("[+] Next handler executed: 0x%08X" % (next_handler))
pass
If we include this code in the script, and we run it, we will obtain an output like the next one:
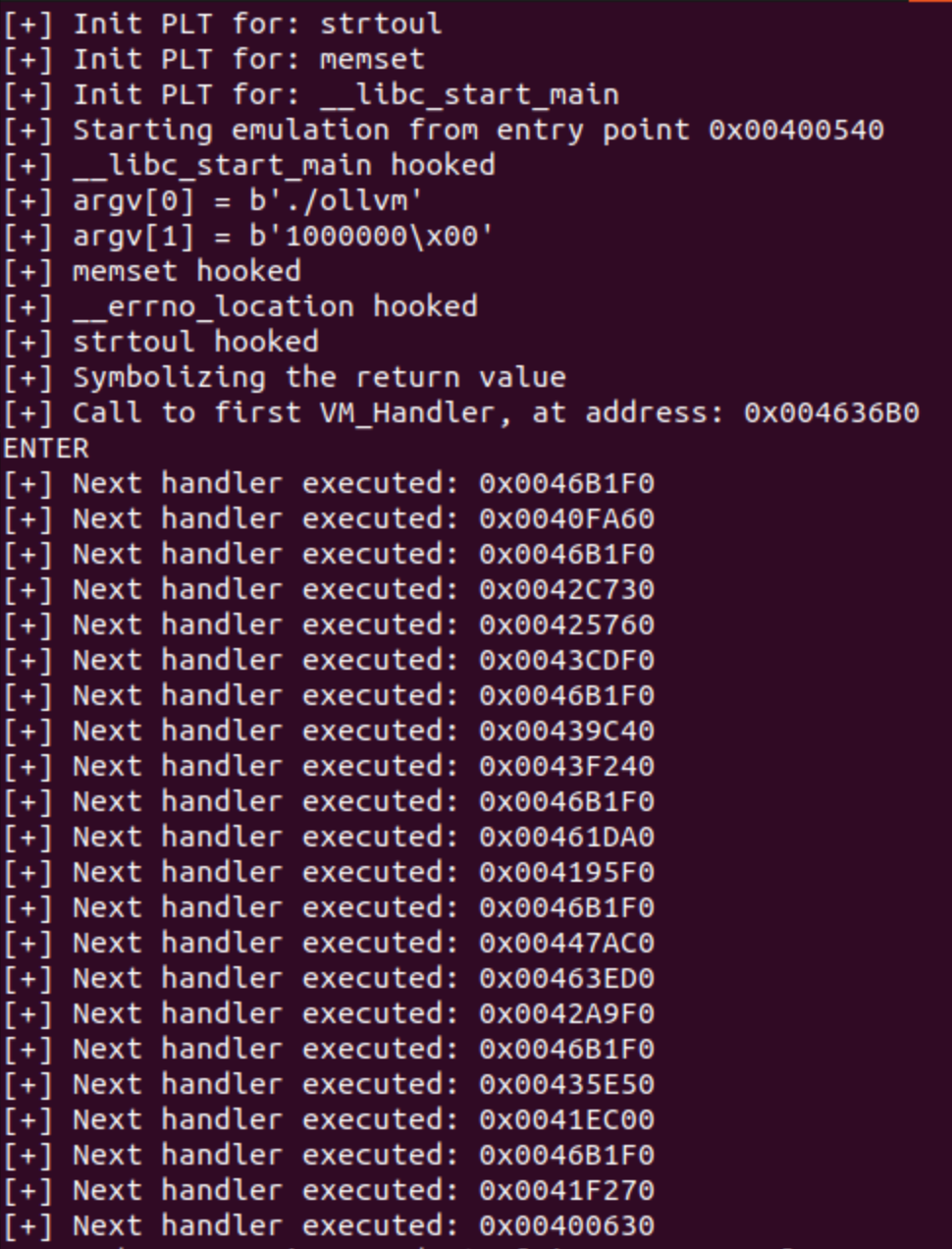
Here we automatically extracted the list of handlers the program runs. Just including a few lines after processing the instruction.
Obtaining the Intermediate expressions
Each of the handlers will calculate a hash that can be used in the subsequent handlers as values to make the final expression harder to reverse. Additionally, they will provide an output that is significantly different from the input value. To determine the complexity of these handlers’ expressions, we can obtain their expressions using the Triton API. For this purpose, I have selected two handlers with addresses 0x0040fa60 and 0x0042C730. For each of these handlers, we will identify the address where the resulting hash is stored:


Since each handler uses RAX as the register, we will inspect each one of the addresses, retrieve the AST expression, and then unroll it with the following code:
def post_execution(previous_pc, instruction, ctx):
'''
Code to call after processing an instruction
'''
...
# analyze newer values pushed into the bytecode
if previous_pc in [0x0040fdab, 0x0042ccf1]:
rax = ctx.getConcreteRegisterValue(ctx.registers.rax)
mem_stored = rax*8 + 0x67b280
ast_mem = ctx.getSymbolicMemory(mem_stored).getAst()
ast = ctx.getAstContext()
print(ast.unroll(ast_mem))
input("ENTER")
...
pass
Running this, we will obtain each one of the expressions for each calculated hash:
[+] Next handler executed: 0x0040FA60
((_ extract 7 0) (bvadd (bvmul ((_ zero_extend 32) (bvand ((_ extract 31 0) (bvshl (bvadd (bvmul (bvsub SymVar_0 SymVar_0) SymVar_0)
(bvand (bvor (bvxor (bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0)
(_ bv18446744073709551614 64)) (_ bv18446744073709551614 64)))) (_ bv2 64)) (bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64))
(bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64)) (_ bv18446744073709551614 64))))) (bvneg (bvsub (bvsub SymVar_0
(_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64)) (_ bv18446744073709551614 64))))))
(bvand ((_ zero_extend 56) ((_ extract 7 0) (bvadd (bvmul (bvsub SymVar_0 SymVar_0) SymVar_0) (bvand (bvor (bvxor (bvneg (bvsub
(bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64))
(_ bv18446744073709551614 64)))) (_ bv2 64)) (bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor
(bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64)) (_ bv18446744073709551614 64))))) (bvneg (bvsub (bvsub SymVar_0
(_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64)) (_ bv18446744073709551614 64))))))))
(_ bv63 64)))) (_ bv1 32))) (_ bv7413137316104562390 64)) (bvadd (bvxor (_ bv12906354758612225394 64) (bvadd (bvmul
(bvsub SymVar_0 SymVar_0) SymVar_0) (bvand (bvor (bvxor (bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64)) (_ bv18446744073709551614 64)))) (_ bv2 64)) (bvneg (bvsub (bvsub SymVar_0
(_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64)) (_ bv18446744073709551614 64)))))
(bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64))
(_ bv18446744073709551614 64))))))) (_ bv10072043083552405557 64))))
[+] Next handler executed: 0x0042C730
((_ extract 7 0) (bvmul (bvshl (bvxor (_ bv14887247549634619895 64) (bvadd (bvmul ((_ zero_extend 32) (bvand ((_ extract 31 0)
(bvshl (bvadd (bvmul (bvsub SymVar_0 SymVar_0) SymVar_0) (bvand (bvor (bvxor (bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64))
(bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64)) (_ bv18446744073709551614 64)))) (_ bv2 64)) (bvneg (bvsub
(bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64))
(_ bv18446744073709551614 64))))) (bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0)
(_ bv18446744073709551614 64)) (_ bv18446744073709551614 64)))))) (bvand ((_ zero_extend 56) ((_ extract 7 0) (bvadd (bvmul
(bvsub SymVar_0 SymVar_0) SymVar_0) (bvand (bvor (bvxor (bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor
(bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64)) (_ bv18446744073709551614 64)))) (_ bv2 64)) (bvneg (bvsub (bvsub SymVar_0
(_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64)) (_ bv18446744073709551614 64))))) (bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64))
(_ bv18446744073709551614 64)))))))) (_ bv63 64)))) (_ bv1 32))) (_ bv7413137316104562390 64)) (bvadd (bvxor (_ bv12906354758612225394 64)
(bvadd (bvmul (bvsub SymVar_0 SymVar_0) SymVar_0) (bvand (bvor (bvxor (bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64))
(bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64)) (_ bv18446744073709551614 64)))) (_ bv2 64)) (bvneg (bvsub
(bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64))
(_ bv18446744073709551614 64))))) (bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0)
(_ bv18446744073709551614 64)) (_ bv18446744073709551614 64))))))) (_ bv10072043083552405557 64)))) (_ bv32 64)) ((_ zero_extend 32)
(bvand (bvnot (bvor (_ bv190 32) (bvnot (bvxor (bvor (bvsub (_ bv4294967289 32) (bvor (_ bv5 32) (bvsub (_ bv4294967294 32)
(bvand (_ bv4 32) (bvor (bvadd (bvor (bvneg ((_ extract 31 0) (bvadd (bvmul ((_ zero_extend 32) (bvand ((_ extract 31 0) (bvshl
(bvadd (bvmul (bvsub SymVar_0 SymVar_0) SymVar_0) (bvand (bvor (bvxor (bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64))
(bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64)) (_ bv18446744073709551614 64)))) (_ bv2 64)) (bvneg (bvsub
(bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64))
(_ bv18446744073709551614 64))))) (bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0)
(_ bv18446744073709551614 64)) (_ bv18446744073709551614 64)))))) (bvand ((_ zero_extend 56) ((_ extract 7 0) (bvadd (bvmul
(bvsub SymVar_0 SymVar_0) SymVar_0) (bvand (bvor (bvxor (bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor
(bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64)) (_ bv18446744073709551614 64)))) (_ bv2 64)) (bvneg (bvsub (bvsub SymVar_0
(_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64)) (_ bv18446744073709551614 64)))))
(bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64))
(_ bv18446744073709551614 64)))))))) (_ bv63 64)))) (_ bv1 32))) (_ bv7413137316104562390 64)) (bvadd (bvxor (_ bv12906354758612225394 64)
(bvadd (bvmul (bvsub SymVar_0 SymVar_0) SymVar_0) (bvand (bvor (bvxor (bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64))
(bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64)) (_ bv18446744073709551614 64)))) (_ bv2 64)) (bvneg (bvsub
(bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0) (_ bv18446744073709551614 64))
(_ bv18446744073709551614 64))))) (bvneg (bvsub (bvsub SymVar_0 (_ bv5610100774807237061 64)) (bvxor (bvxor (bvadd SymVar_0 SymVar_0)
(_ bv18446744073709551614 64)) (_ bv18446744073709551614 64))))))) (_ bv10072043083552405557 64))))) (_ bv8557572 32)) (_ bv1 32))
(_ bv8525316 32)))))) (_ bv244 32)) (_ bv91 32))))) (_ bv91 32)))))
From the previous output, we can observe that we obtain a complex AST that would likely be difficult to solve manually.
However, we do not need to solve this complex AST, as it is unnecessary to solve the challenge. Instead, we only need the last expression retrieved from the main function.
Solving the Challenge
In this challenge, we are provided with a given value as input and an output generated by the program. Based on information gathered from researching the challenge and examining Jonathan’s script, our task is to find eight input values that produce the following hashes as output: 0x875cd4f2e18f8fc4, 0xbb093e17e5d3fa42, 0xada5dd034aae16b4, 0x97322728fea51225, 0x4124799d72188d0d, 0x2b3e3fbbb4d44981, 0xdfcac668321e4daa, and 0xeac2137a35c8923a. The process will be as follows:
- Symbolize the output from
strtoulto work with a symbolic value. - Execute the handlers until the program returns to the
mainfunction. - Extract the expression from the parameter of the
printffunction. - Transform the expression to
Z3format. - Inject each of the hashes as a constraint and solve the challenge.
As mentioned before, we already saw the code for setting the output of strtoul as symbolic:
def strtoul(ctx):
'''
Hook for strtoul
'''
print('[+] strtoul hooked')
return (SYMBOLIC, int("0xdeadbeef", 16))
With this, the concrete value 0xdeadbeef will be set in RAX and the operations with the value will be tracked. Then we just need to keep emulating for running the different handlers. Then we will stop the emulation after running the next instruction:

At address 0x004008d3, the program retrieves the resulting hash from one memory location. This is the instruction where we will stop in the post_execution function. The value is moved to the RSI register, which Ghidra renames as argv. We will then retrieve the full expression from RSI, and for each of the previous hash values, we will create rounds with different constraints.
hashes_to_check = [
0x875cd4f2e18f8fc4,
0xbb093e17e5d3fa42,
0xada5dd034aae16b4,
0x97322728fea51225,
0x4124799d72188d0d,
0x2b3e3fbbb4d44981,
0xdfcac668321e4daa,
0xeac2137a35c8923a
]
def post_execution(previous_pc, instruction, ctx):
'''
Code to call after processing an instruction
'''
...
if previous_pc == 0x004008d3:
print(str(instruction))
flag=""
rsi = ctx.getRegisterAst(ctx.registers.rsi)
ast = ctx.getAstContext()
for hash_to_check in hashes_to_check:
model = myExternalSolver(
ctx, rsi == hash_to_check, previous_pc)
for k, v in list(model.items()):
print("Value %d in decimal: 0x%08X for hash %08x" %
(k, v, hash_to_check))
flag += bytes.fromhex(hex(v).replace('0x','')).decode('utf-8')
print(f"Flag {flag}")
pass
I am using here the same function that we saw at the end of the previous post, myExternalSolver. These functions are used for generating the Z3 expressions and solving them to obtain the flag:
def getVarSyntax(ctx):
'''
Retrieve all the declared symbolic variables
and generatae them as a string like the next:
(declare-fun SymVar_0 () (_ BitVec 8))
:param ctx: triton context for using utilities
'''
s = str()
ast = ctx.getAstContext()
for k, v in list(ctx.getSymbolicVariables().items()):
s += str(ast.declare(ast.variable(v))) + '\n'
return s
def getSSA(ctx, expr):
'''
Get an SSA version of the expression given as parameter
this will generate all the expressions in an IR form
with SSA form.
:param ctx: triton context for using utilities
:param expr: expression to retrieve its SSA form
'''
s = str()
# current AST of the program
ast = ctx.getAstContext()
# generate an IR in SSA from the expression
ssa = ctx.sliceExpressions(expr)
for k, v in sorted(ssa.items())[:-1]:
s += str(v) + '\n'
s += str(ast.assert_(expr.getAst())) + '\n'
return s
def myExternalSolver(ctx, node, addr=None, debug=False):
"""
The particularity of this sample is that we use an external solver to solve
queries instead of using the internal Triton's solver (even if in both cases
it uses z3). The point here is to show that Triton can provide generic smt2
outputs and theses outputs can be send to external solvers and get back model
which then are sent to Triton.
"""
import z3
expr = ctx.newSymbolicExpression(node, "Custom for Solver")
varSyntax = getVarSyntax(ctx)
ssa = getSSA(ctx, expr)
smtFormat = '(set-logic QF_BV) %s %s (check-sat) (get-model)' % (
varSyntax, ssa)
if debug:
print(smtFormat)
c = z3.Context()
s = z3.Solver(ctx=c)
s.add(z3.parse_smt2_string(smtFormat, ctx=c))
if addr:
print('[+] Solving condition at %#x' % (addr))
if s.check() == z3.sat:
ret = dict()
model = s.model()
for x in model:
if not "ref" in str(x):
ret.update(
{int(str(x).split('_')[1], 10): int(str(model[x]), 10)})
else:
continue
return ret
else:
print('[-] unsat :(')
sys.exit(-1)
return
Now we have all the different pieces for obtaining the output flag:
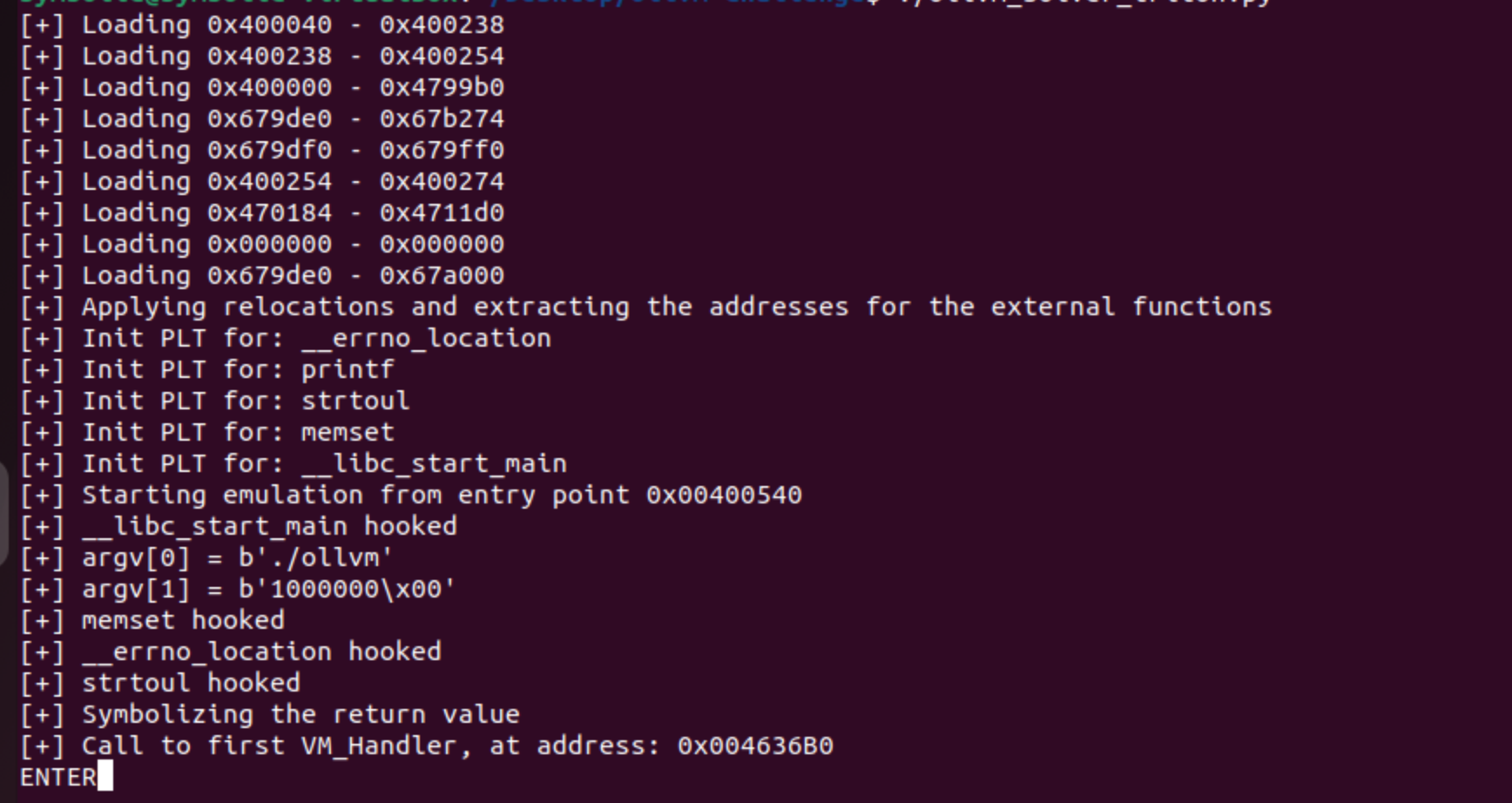
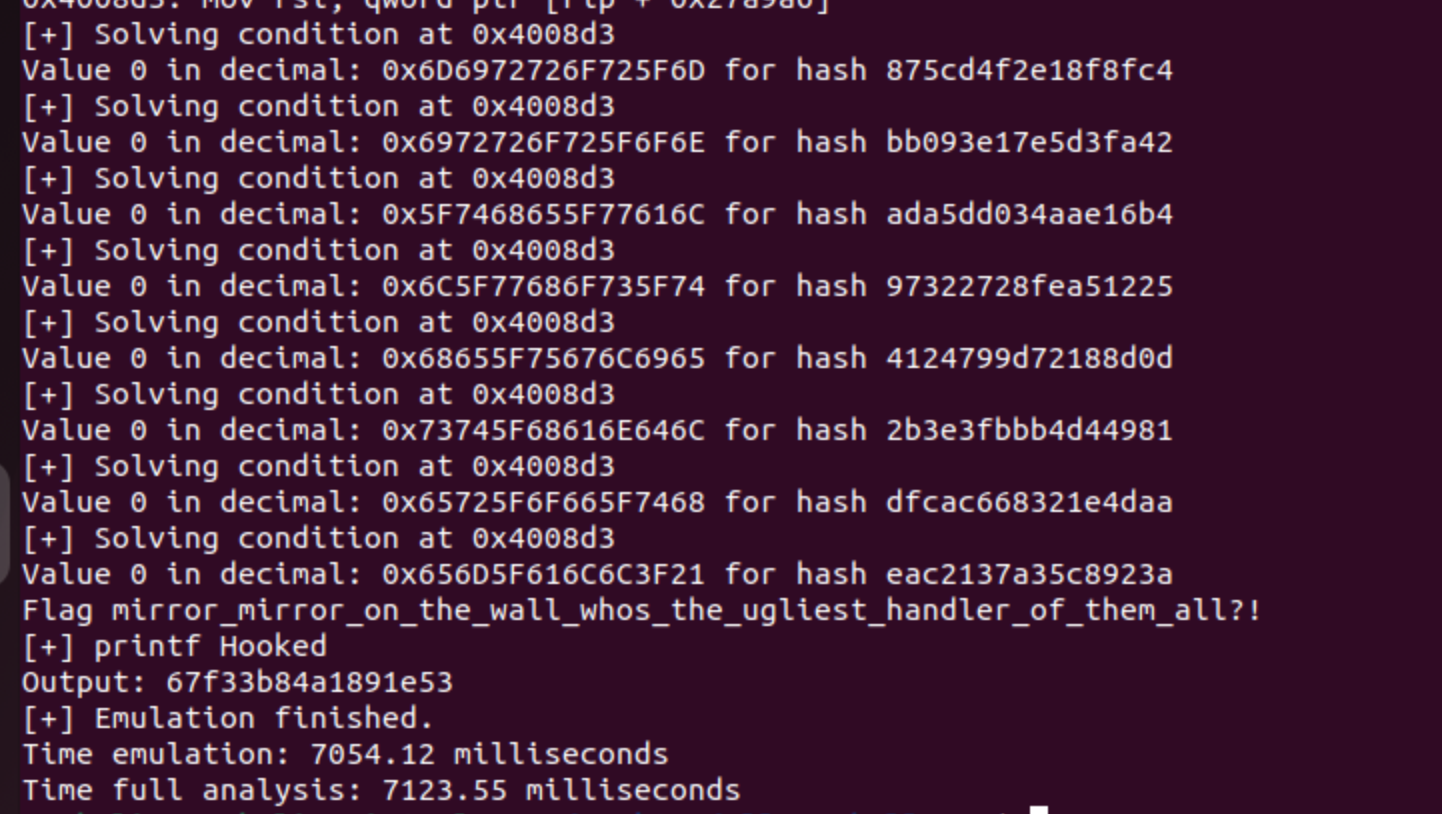
We have solved the expression for each one of the hashes, and we finally obtained the Flag: mirror_mirror_on_the_wall_whos_the_ugliest_handler_of_them_all?!, and with this we would have finished the challenge!
LLVM IR and Cleaning the Expression
Before concluding this post, I will show a couple of interesting things. Triton uses an Abstract Syntax Tree (AST) internally to keep track of the symbolic expression, but it allows lifting this AST to LLVM IR. LLVM is a compiler framework that works with a comprehensive Intermediate Representation (IR), enabling the representation of high-level code and allowing the application of various compiler optimizations. Utilizing LLVM IR can be beneficial for analyzing binary code, as we can directly apply these optimizations to the IR instead of the assembly code. Another intriguing feature of Triton is the ability to apply optimizations to the generated IR. We will include the following code in the solution for the challenge:
def post_execution(previous_pc, instruction, ctx):
'''
Code to call after processing an instruction
'''
if previous_pc == 0x004008d3:
print(str(instruction))
flag=""
rsi = ctx.getRegisterAst(ctx.registers.rsi)
ast = ctx.getAstContext()
M = ctx.liftToLLVM(rsi, fname="expression_ollvm", optimize=False)
print("Not simplified RSI:")
print(M)
M = ctx.liftToLLVM(rsi, fname="expression_ollvm", optimize=True)
print("Simplified RSI Through LLVM:")
print(M)
for hash_to_check in hashes_to_check:
model = myExternalSolver(
ctx, rsi == hash_to_check, previous_pc)
for k, v in list(model.items()):
print("Value %d in decimal: 0x%08X for hash %08x" %
(k, v, hash_to_check))
flag += bytes.fromhex(hex(v).replace('0x','')).decode('utf-8')
print(f"Flag {flag}")
pass
The Not simplified expression is the next one:
; ModuleID = 'tritonModule'
source_filename = "tritonModule"
define i64 @expression_ollvm(i64 %SymVar_0) {
entry:
%0 = add i64 %SymVar_0, %SymVar_0
%1 = xor i64 %0, -2
%2 = xor i64 %1, -2
%3 = sub i64 %SymVar_0, 5610100774807237061
%4 = sub i64 %3, %2
%5 = sub i64 0, %4
%6 = xor i64 %5, 2
%7 = or i64 %6, %5
%8 = and i64 %7, %5
%9 = sub i64 %SymVar_0, %SymVar_0
%10 = mul i64 %9, %SymVar_0
%11 = add i64 %10, %8
%12 = xor i64 -5540389315097326222, %11
%13 = add i64 %12, -8374700990157146059
%14 = trunc i64 %11 to i8
%15 = zext i8 %14 to i64
%16 = and i64 %15, 63
%17 = shl i64 %11, %16
%18 = trunc i64 %17 to i32
%19 = and i32 %18, 1
%20 = zext i32 %19 to i64
%21 = mul i64 %20, 7413137316104562390
%22 = add i64 %21, %13
%23 = xor i64 -3559496524074931721, %22
%24 = shl i64 %23, 32
%25 = lshr i64 %23, 32
%26 = xor i64 %22, -1
%27 = and i64 %26, -3559496524074931721
%28 = and i64 3559496524074931720, %22
%29 = trunc i64 %28 to i32
%30 = and i32 %29, 2
%31 = zext i32 %30 to i64
%32 = sub i64 0, %31
%33 = add i64 -1, %31
%34 = and i64 %28, %32
%35 = or i64 %34, %33
%36 = xor i64 %35, %28
%37 = and i64 %36, %32
%38 = or i64 %37, %28
%39 = sub i64 %38, %31
%40 = or i64 %39, %28
%41 = add i64 %40, %27
%42 = shl i64 %41, 32
%43 = xor i64 %42, -1
%44 = or i64 %43, %24
%45 = xor i64 %44, %25
%46 = xor i64 %45, -1
%47 = trunc i64 %23 to i32
%48 = and i32 %47, 63
%49 = trunc i32 %48 to i8
%50 = zext i8 %49 to i64
%51 = and i64 %50, 63
%52 = shl i64 32, %51
%53 = trunc i64 %52 to i32
%54 = and i32 %53, %48
%55 = trunc i32 %54 to i8
%56 = zext i8 %55 to i64
%57 = and i64 %56, 63
%58 = shl i64 32, %57
%59 = trunc i64 %58 to i8
%60 = zext i8 %59 to i64
%61 = and i64 %60, 63
%62 = shl i64 %23, %61
%63 = or i64 %62, %46
%64 = xor i64 %24, -1
%65 = and i64 %64, %63
%66 = xor i64 %65, %24
%67 = trunc i64 %66 to i32
%68 = zext i32 %67 to i64
%69 = or i64 %68, -2
%70 = and i64 %66, %69
%71 = mul i64 -6464709178843836683, %70
%72 = add i64 %71, 1779491018601202359
%73 = and i64 %72, %72
%74 = icmp eq i64 %73, 0
%75 = select i1 %74, i1 true, i1 false
%76 = icmp eq i1 %75, true
%77 = select i1 %76, i64 56, i64 0
%78 = add i64 %77, 3179662501
%79 = xor i64 -3559496524074931721, %22
%80 = lshr i64 %79, 32
%81 = trunc i64 %80 to i32
%82 = trunc i64 %80 to i32
%83 = mul i32 %82, %81
%84 = trunc i32 %83 to i8
%85 = and i8 %84, 2
%86 = zext i8 %85 to i64
%87 = and i64 %86, 63
%88 = trunc i64 %22 to i32
%89 = sub i32 0, %88
%90 = or i32 %89, 8557572
%91 = add i32 %90, 1
%92 = or i32 %91, 8525316
%93 = and i32 4, %92
%94 = sub i32 -2, %93
%95 = or i32 5, %94
%96 = sub i32 -7, %95
%97 = or i32 %96, 244
%98 = xor i32 %97, 91
%99 = xor i32 %98, -1
%100 = or i32 190, %99
%101 = xor i32 %100, -1
%102 = and i32 %101, 91
%103 = zext i32 %102 to i64
%104 = xor i64 -3559496524074931721, %22
%105 = shl i64 %104, 32
%106 = mul i64 %105, %103
%107 = mul i64 %106, 2
%108 = xor i64 %106, -1
%109 = add i64 %108, %107
%110 = add i64 %109, 1
%111 = or i64 %110, %106
%112 = add i64 %111, -1
%113 = and i64 %112, %80
%114 = xor i64 %113, %106
%115 = or i64 %114, %80
%116 = add i64 -1, %106
%117 = and i64 %116, %80
%118 = xor i64 %117, %106
%119 = or i64 %118, %80
%120 = add i64 %119, 1
%121 = add i64 %118, %106
%122 = trunc i64 %80 to i32
%123 = and i32 %122, 2
%124 = zext i32 %123 to i64
%125 = xor i64 %124, 2
%126 = and i64 %125, %80
%127 = or i64 %126, %106
%128 = add i64 %127, -1
%129 = and i64 %128, %80
%130 = xor i64 %129, %106
%131 = sub i64 %130, %108
%132 = xor i64 %118, -1
%133 = add i64 %132, %108
%134 = xor i64 %133, %106
%135 = xor i64 %134, %131
%136 = add i64 %135, %121
%137 = add i64 %136, 1
%138 = or i64 %137, %80
%139 = and i64 %138, %120
%140 = or i64 %139, %115
%141 = shl i64 %140, %87
%142 = mul i64 %141, -6464709178843836683
%143 = mul i64 2, %142
%144 = sub i64 0, %142
%145 = add i64 %144, %143
%146 = trunc i64 %145 to i8
%147 = zext i8 %146 to i64
%148 = and i64 %147, 63
%149 = shl i64 %145, %148
%150 = trunc i64 %149 to i32
%151 = and i32 %150, 1
%152 = zext i32 %151 to i64
%153 = or i64 %152, -52618
%154 = add i64 %153, 52617
%155 = ashr i64 %154, 63
%156 = add i64 1779491018601202359, %145
%157 = lshr i64 %156, 8
%158 = mul i64 %157, %155
%159 = sub i64 0, %158
%160 = shl i64 %159, 54
%161 = trunc i64 %160 to i32
%162 = and i32 %161, 689829814
%163 = and i32 %162, 1
%164 = zext i32 %163 to i64
%165 = xor i64 %164, 689829814
%166 = xor i64 %165, -1
%167 = and i64 689829813, %166
%168 = xor i64 %167, -1
%169 = or i64 %168, 2
%170 = add i64 %169, -2
%171 = xor i64 %170, -1
%172 = lshr i64 %171, 63
%173 = mul i64 %172, %78
%174 = trunc i64 %72 to i32
%175 = add i64 -1, %72
%176 = trunc i64 %175 to i32
%177 = and i32 %176, %174
%178 = and i32 %177, 1
%179 = xor i32 %178, 63
%180 = and i32 56, %179
%181 = trunc i32 %180 to i8
%182 = zext i8 %181 to i64
%183 = and i64 %182, 63
%184 = shl i64 %72, %183
%185 = or i64 %184, %159
%186 = mul i64 %185, -1
%187 = sub i64 0, %186
%188 = add i64 %187, %173
%189 = xor i64 %188, 3633819531175615211
%190 = add i64 %189, 3014537922511877372
%191 = mul i64 -1, %190
%192 = sub i64 0, %191
%193 = or i64 %191, %192
%194 = xor i64 %192, %191
%195 = and i64 %194, %193
%196 = xor i64 %188, -3633819531175615212
%197 = add i64 -1, %188
%198 = and i64 %197, %188
%199 = sub i64 0, %188
%200 = and i64 %199, %188
%201 = xor i64 -3633819531175615212, %200
%202 = xor i64 %201, %198
%203 = or i64 %202, %189
%204 = xor i64 %203, %196
%205 = add i64 %204, 3014537922511877372
%206 = add i64 %205, %205
%207 = sub i64 %206, %190
%208 = mul i64 %207, -1
%209 = xor i64 %208, %195
%210 = trunc i64 %209 to i8
%211 = zext i8 %210 to i64
%212 = and i64 %211, 63
%213 = shl i64 %209, %212
%214 = trunc i64 %213 to i32
%215 = and i32 %214, 1
%216 = zext i32 %215 to i64
%217 = xor i64 -3, %216
%218 = add i64 -2, %217
%219 = and i64 %218, %217
%220 = xor i64 -3, %216
%221 = or i64 %220, %219
%222 = add i64 %221, 2
%223 = xor i64 -3, %216
%224 = or i64 %223, %219
%225 = add i64 %224, 2
%226 = and i64 -71777214294589693, %225
%227 = or i64 %226, %222
%228 = shl i64 %209, 8
%229 = and i64 %228, -71777214294589696
%230 = mul i64 %229, %227
%231 = sub i64 0, %230
%232 = add i64 %231, %231
%233 = shl i64 %232, 20
%234 = trunc i64 %233 to i32
%235 = xor i32 %234, -1
%236 = or i32 %235, -2
%237 = and i32 %236, 27293611
%238 = zext i32 %237 to i64
%239 = add i64 %238, -1
%240 = ashr i64 %239, 63
%241 = and i64 %240, -4611686018427387904
%242 = xor i64 %241, -1
%243 = add i64 %242, %240
%244 = xor i64 %243, -1
%245 = add i64 %244, %240
%246 = lshr i64 %209, 8
%247 = trunc i64 %246 to i32
%248 = and i32 %247, 63
%249 = trunc i32 %248 to i8
%250 = zext i8 %249 to i64
%251 = and i64 %250, 63
%252 = shl i64 1, %251
%253 = trunc i64 %252 to i32
%254 = and i32 %248, %253
%255 = trunc i32 %254 to i8
%256 = zext i8 %255 to i64
%257 = and i64 %256, 63
%258 = shl i64 %246, %257
%259 = and i64 %258, 71777214294589695
%260 = or i64 %259, 2
%261 = xor i64 %260, -1
%262 = or i64 %259, -3
%263 = add i64 %259, %259
%264 = xor i64 %263, -1
%265 = add i64 %264, %259
%266 = xor i64 %265, %262
%267 = and i64 %266, %259
%268 = xor i64 %267, %260
%269 = or i64 %268, %261
%270 = sub i64 %260, %259
%271 = xor i64 %270, %259
%272 = and i64 %260, %259
%273 = and i64 %272, %271
%274 = add i64 %273, %269
%275 = trunc i64 %259 to i32
%276 = trunc i64 %259 to i32
%277 = mul i32 %276, %275
%278 = and i32 %277, 2
%279 = xor i64 %259, -1
%280 = trunc i64 %279 to i32
%281 = or i32 %280, %278
%282 = zext i32 %281 to i64
%283 = xor i64 %231, -1
%284 = or i64 %283, %259
%285 = add i64 %284, %282
%286 = trunc i64 %285 to i32
%287 = add i32 %286, 1
%288 = trunc i64 %259 to i32
%289 = trunc i64 %284 to i32
%290 = trunc i64 %259 to i32
%291 = trunc i64 %231 to i32
%292 = xor i32 %291, -1
%293 = or i32 %292, %290
%294 = and i32 %293, 2
%295 = or i32 %294, %289
%296 = sub i32 %295, %288
%297 = mul i32 %296, %287
%298 = and i32 %297, 2
%299 = zext i32 %298 to i64
%300 = add i64 %284, %279
%301 = xor i64 %300, -1
%302 = or i64 %301, %299
%303 = add i64 %302, %274
%304 = or i64 %303, %231
%305 = sub i64 0, %245
%306 = or i64 %304, %305
%307 = xor i64 %306, -1
%308 = or i64 %307, %304
%309 = mul i64 -1, %304
%310 = sub i64 0, %309
%311 = or i64 %310, %305
%312 = and i64 %304, %311
%313 = and i64 %312, %308
%314 = add i64 %313, %245
%315 = xor i64 -5064113576967571667, %314
%316 = mul i64 %315, 5906144455206004469
%317 = sub i64 0, %316
%318 = add i64 %316, -1
%319 = or i64 %318, 1
%320 = sub i64 0, %319
%321 = and i64 %320, %317
ret i64 %321
}
And the simplified expression is the next one:
; ModuleID = 'tritonModule'
source_filename = "tritonModule"
; Function Attrs: norecurse nounwind readnone willreturn
define i64 @expression_ollvm(i64 %SymVar_0) local_unnamed_addr #0 {
entry:
%.neg.neg = shl i64 %SymVar_0, 1
%.neg1 = sub i64 5610100774807237061, %SymVar_0
%.neg2 = add i64 %.neg.neg, %.neg1
%0 = xor i64 %.neg2, -5540389315097326222
%1 = add i64 %0, -8374700990157146059
%2 = and i64 %.neg2, 63
%3 = shl i64 %.neg2, %2
%4 = and i64 %3, 1
%5 = mul nuw nsw i64 %4, 7413137316104562390
%6 = add i64 %1, %5
%7 = xor i64 %6, -3559496524074931721
%8 = shl i64 %7, 32
%9 = shl i64 %6, 32
%10 = xor i64 %9, -3983057798777798657
%11 = or i64 %10, %8
%12 = lshr i64 %6, 32
%13 = xor i64 %12, %11
%14 = xor i64 %13, -3466207430
%15 = and i64 %7, 63
%16 = shl i64 32, %15
%17 = and i64 %15, %16
%18 = shl i64 32, %17
%19 = and i64 %18, 63
%20 = shl i64 %7, %19
%21 = or i64 %14, %8
%22 = or i64 %21, %20
%23 = xor i64 %12, 3466207429
%24 = trunc i64 %23 to i8
%25 = mul i8 %24, %24
%26 = and i8 %25, 2
%27 = zext i8 %26 to i64
%28 = xor i64 %9, 3983057798777798656
%29 = or i64 %23, %28
%30 = add i64 %29, 1
%31 = and i64 %12, 2
%32 = xor i64 %31, 2
%33 = and i64 %32, %12
%34 = add nuw nsw i64 %33, 4294967295
%35 = and i64 %34, %23
%36 = sub i64 %28, %10
%37 = add i64 %36, %35
%38 = xor i64 %29, -1
%39 = add i64 %10, %38
%40 = xor i64 %39, %28
%41 = xor i64 %40, %37
%42 = add i64 %30, %28
%43 = add i64 %42, %41
%44 = or i64 %43, %23
%45 = and i64 %44, %30
%46 = or i64 %45, %29
%47 = shl i64 %46, %27
%48 = mul i64 %47, -6464709178843836683
%49 = and i64 %48, 63
%50 = shl i64 %48, %49
%51 = and i64 %50, 1
%52 = add nuw nsw i64 %51, 72057594037927935
%53 = add i64 %48, 1779491018601202359
%54 = lshr i64 %53, 8
%.neg3 = and i64 %52, %54
%.neg.neg6 = mul i64 %22, -792633534417207296
%.neg4.neg = add i64 %.neg.neg6, -5260204364768739328
%.neg5.neg = or i64 %.neg3, %.neg4.neg
%55 = xor i64 %.neg5.neg, 3633819531175615211
%.neg = add i64 %55, 3014537922511877372
%56 = sub i64 -3014537922511877372, %55
%57 = xor i64 %.neg, %56
%58 = xor i64 %.neg5.neg, 5589552505679160596
%59 = or i64 %58, %55
%60 = xor i64 %59, %.neg5.neg
%61 = shl i64 %60, 1
%62 = xor i64 %61, 7267639062351230423
%63 = add i64 %55, -3014537922511877371
%.neg7 = add i64 %63, %62
%64 = xor i64 %57, %.neg7
%65 = and i64 %64, 63
%66 = shl i64 %64, %65
%67 = and i64 %66, 1
%.neg10 = add nuw nsw i64 %67, 1
%68 = shl i64 %64, 8
%69 = and i64 %68, -71777214294589696
%.neg11 = mul i64 %.neg10, %69
%70 = lshr i64 %64, 8
%71 = and i64 %70, 63
%72 = shl nuw i64 1, %71
%73 = and i64 %71, %72
%74 = shl i64 %70, %73
%75 = and i64 %74, 71777214294589695
%76 = or i64 %75, 2
%77 = xor i64 %76, -1
%78 = or i64 %74, 71777214294589693
%79 = shl nuw nsw i64 %75, 1
%80 = xor i64 %79, -1
%81 = add nsw i64 %75, %80
%82 = xor i64 %81, %78
%83 = and i64 %82, %74
%84 = xor i64 %83, %76
%85 = or i64 %84, %77
%86 = add nsw i64 %75, %77
%87 = and i64 %86, %75
%88 = add nsw i64 %85, %87
%89 = trunc i64 %75 to i32
%90 = mul i32 %89, %89
%91 = and i32 %90, 2
%92 = xor i32 %89, -1
%93 = or i32 %91, %92
%94 = xor i64 %.neg11, -1
%95 = or i64 %75, %94
%96 = trunc i64 %95 to i32
%97 = add i32 %96, 1
%98 = add i32 %97, %93
%99 = sub i32 %96, %89
%100 = mul i32 %98, %99
%101 = and i32 %100, 2
%102 = zext i32 %101 to i64
%103 = sub i64 %75, %95
%104 = or i64 %103, %102
%105 = add i64 %88, %104
%106 = or i64 %105, %.neg11
%107 = xor i64 %106, -5064113576967571667
%108 = mul i64 %107, 5906144455206004469
%109 = sub i64 0, %108
%110 = add i64 %108, -1
%111 = or i64 %110, 1
%112 = sub nsw i64 0, %111
%113 = and i64 %112, %109
ret i64 %113
}
In this case, the LLVM optimizer has been able to reduce the number of variables from 321 to 113. Once again, the final expression contains various arithmetic and logical instructions, as it also employs MBA obfuscation. To further clean the output, we will save the first LLVM IR into a file, and then use SiMBA-, which is a C++ MBA Solver. There is a previous version in Python, SiMBA, which claims to be an Efficient Deobfuscation of Linear Mixed Boolean-Arithmetic Expressions, as stated on their GitHub repository. More information can be found in their paper. In this case, it will be a simple test to obtain a simpler view of the expression:
$ ./SiMBA++ -fastcheck -bitcount=64 -optimize=true -detect-simplify -ir /home/symbolic/Desktop/ollvm-challenge/LLVM-Files/expression_ollvm_opt.ll -out /home/symbolic/Desktop/ollvm-challenge/LLVM-Files/expression_ollvm_opt.simplify.ll
_____ __ ______ ___ __ __
/ __(_) |/ / _ )/ _ |__/ /___/ /_
_\ \/ / /|_/ / _ / __ /_ __/_ __/
/___/_/_/ /_/____/_/ |_|/_/ /_/1.0
°°SiMBA ported to C/C++/LLVM ~pgarba~
[+] Loading LLVM Module: '/home/symbolic/Desktop/ollvm-challenge/LLVM-Files/expression_ollvm_opt.ll'
[+] Running LLVM optimizer (Some MBAs might already be simplified by that!) ... Done! (23 ms)
[+] Running LLVM optimizer ... Done! (6 ms)
[+] Wrote LLVM Module to: '/home/symbolic/Desktop/ollvm-challenge/LLVM-Files/expression_ollvm_opt.simplify.ll'
[+] MBAs found and replaced: '9' time: 166ms
The C++ version of SiMBA allows to provide the engine with an LLVM IR file as input, and then another one will be generated with the simplified expression, the output is the next one:
; Function Attrs: mustprogress nofree norecurse nosync nounwind willreturn memory(none)
define i64 @mba(i64 %SymVar_0) local_unnamed_addr #0 {
entry:
%0 = add i64 %SymVar_0, 5610100774807237061
%1 = xor i64 %0, -5540389315097326222
%2 = add i64 %1, -8374700990157146059
%3 = shl i64 %2, 32
%4 = lshr i64 %2, 32
%5 = or i64 %4, %3
%6 = xor i64 %5, 3983057802244006085
%7 = xor i64 %4, 3466207429
%8 = xor i64 %3, 3983057798777798656
%9 = or i64 %7, %8
%10 = add i64 %9, 1
%11 = xor i64 %3, -3983057798777798657
%12 = add i64 %11, %8
%13 = add i64 %12, %10
%14 = or i64 %13, %7
%15 = and i64 %14, %10
%16 = or i64 %8, %15
%17 = or i64 %16, %7
%18 = mul i64 %17, -6464709178843836683
%19 = add i64 %18, 1779491018601202359
%20 = lshr i64 %19, 8
%.neg4.neg = mul i64 %6, -792633534417207296
%.neg5.neg = add i64 %.neg4.neg, -5260204364768739328
%.neg6.neg = or i64 %20, %.neg5.neg
%21 = xor i64 %.neg6.neg, 3633819531175615211
%.neg7 = add i64 %21, 3014537922511877372
%22 = sub i64 -3014537922511877372, %21
%23 = xor i64 %.neg7, %22
%24 = xor i64 %.neg6.neg, 5589552505679160596
%25 = or i64 %24, %21
%26 = xor i64 %25, %.neg6.neg
%27 = shl i64 %26, 1
%.neg9.neg = xor i64 %27, 7267639062351230423
%.neg11 = add i64 %21, -3014537922511877371
%28 = add i64 %.neg11, %.neg9.neg
%29 = xor i64 %23, %28
%30 = and i64 %29, 63
%31 = shl i64 %29, %30
%32 = and i64 %31, 1
%.neg12 = add nuw nsw i64 %32, 1
%33 = shl i64 %29, 8
%34 = and i64 %33, -71777214294589696
%.neg13 = mul i64 %.neg12, %34
%35 = lshr i64 %29, 8
%36 = and i64 %35, 63
%37 = shl nuw i64 1, %36
%38 = and i64 %37, %36
%39 = shl i64 %35, %38
%40 = and i64 %39, 71777214294589695
%41 = or i64 %40, 2
%42 = or i64 %39, 71777214294589693
%43 = shl nuw nsw i64 %40, 1
%44 = xor i64 %43, -1
%45 = add nsw i64 %40, %44
%46 = xor i64 %45, %42
%47 = and i64 %39, %46
%48 = and i64 %47, %41
%49 = xor i64 %48, -1
%50 = xor i64 %41, -1
%51 = add nsw i64 %40, %50
%52 = and i64 %51, %40
%53 = xor i64 %.neg13, -1
%54 = or i64 %40, %53
%55 = sub i64 %40, %54
%56 = add i64 %55, %52
%57 = add i64 %56, %49
%58 = or i64 %57, %.neg13
%59 = xor i64 %58, -5064113576967571667
%60 = mul i64 %59, 5906144455206004469
%61 = sub i64 0, %60
%62 = add i64 %60, -1
%63 = or i64 %62, 1
%64 = sub nsw i64 0, %63
%65 = and i64 %64, %61
ret i64 %65
}
In this case, SiMBA was able to reduce the output from the lifted expression. All these files can be compiled into a binary, we can do it in a very simple way. First of all we will have a very simple C code that we will compile to LLVM IR.
/***
* A simple file to be compiled to LLVM IR
* and then copy the different expressions
* into it for compiling a final file.
*/
#include <stdio.h>
long func(long symbol)
{
return symbol + 5 + 2 * 4;
}
int main(int argc, char **argv)
{
printf("This is just a test: %ld\n", func(argc));
return argc;
}
Now we have to compile it just until generating the LLVM IR, for doing that we will need to use Clang, since is the front-end that LLVM offers for compilation of C code:
$clang-16 -S -emit-llvm simple_file.c -o simple_file.ll
That will provide us with the next LLVM IR code:
; ModuleID = 'simple_file.c'
source_filename = "simple_file.c"
target datalayout = "e-m:e-p270:32:32-p271:32:32-p272:64:64-i64:64-f80:128-n8:16:32:64-S128"
target triple = "x86_64-pc-linux-gnu"
@.str = private unnamed_addr constant [26 x i8] c"This is just a test: %ld\0A\00", align 1
; Function Attrs: noinline nounwind optnone uwtable
define dso_local i64 @func(i64 noundef %0) #0 {
%2 = alloca i64, align 8
store i64 %0, ptr %2, align 8
%3 = load i64, ptr %2, align 8
%4 = add nsw i64 %3, 5
%5 = add nsw i64 %4, 8
ret i64 %5
}
; Function Attrs: noinline nounwind optnone uwtable
define dso_local i32 @main(i32 noundef %0, ptr noundef %1) #0 {
%3 = alloca i32, align 4
%4 = alloca i32, align 4
%5 = alloca ptr, align 8
store i32 0, ptr %3, align 4
store i32 %0, ptr %4, align 4
store ptr %1, ptr %5, align 8
%6 = load i32, ptr %4, align 4
%7 = sext i32 %6 to i64
%8 = call i64 @func(i64 noundef %7)
%9 = call i32 (ptr, ...) @printf(ptr noundef @.str, i64 noundef %8)
%10 = load i32, ptr %4, align 4
ret i32 %10
}
declare i32 @printf(ptr noundef, ...) #1
attributes #0 = { noinline nounwind optnone uwtable "frame-pointer"="all" "min-legal-vector-width"="0" "no-trapping-math"="true" "stack-protector-buffer-size"="8" "target-cpu"="x86-64" "target-features"="+cx8,+fxsr,+mmx,+sse,+sse2,+x87" "tune-cpu"="generic" }
attributes #1 = { "frame-pointer"="all" "no-trapping-math"="true" "stack-protector-buffer-size"="8" "target-cpu"="x86-64" "target-features"="+cx8,+fxsr,+mmx,+sse,+sse2,+x87" "tune-cpu"="generic" }
!llvm.module.flags = !{!0, !1, !2, !3, !4}
!llvm.ident = !{!5}
!0 = !{i32 1, !"wchar_size", i32 4}
!1 = !{i32 8, !"PIC Level", i32 2}
!2 = !{i32 7, !"PIE Level", i32 2}
!3 = !{i32 7, !"uwtable", i32 2}
!4 = !{i32 7, !"frame-pointer", i32 2}
!5 = !{!"Ubuntu clang version 16.0.6 (++20230710042027+7cbf1a259152-1~exp1~20230710162048.105)"}
We just need to replace @func with any of the previously generated functions of LLVM IR, and compile it with the next command:
$ clang-16 simple_file.ll -o simple_file
This binary can be run and also loaded in Ghidra for the analysis, in my case I have done different tests with compilation flags, and with the optimizations that Triton offers:

And with this we can continue doing the analysis of the simplified codes, and also with this I conclude the post!
Extra
Looking for the constants from the binary, I have found another interesting solution posted in here, where the algorithm was reversed, and bruteforcing some of the parameters in the algorithm the correct input value can be calculated, while I think it does not exactly retrieves the inverse hash, it is another solution that would work. In the website, the provided code is for Windows, but next I provide a C++ version that it also works:
#include <iostream>
#include <unistd.h>
std::uint64_t g_chunk_size = 0;
std::uint64_t g_jieguo = 0;
std::uint64_t g_chengshu = 0;
bool g_finded_low = false;
std::uint64_t g_find_val_low = 0;
bool g_finded_high = false;
std::uint64_t g_find_val_high = 0;
std::uint32_t CalcThread(void * start_v) {
std::uint64_t ustartv = (std::uint64_t) start_v;
std::uint32_t targetv = g_jieguo & 0xFFFFFFFF;
std::uint32_t chengshulow = g_chengshu & 0xFFFFFFFF;
for (std::uint64_t i = 0; i < g_chunk_size; i++) {
if (
(((ustartv + i) * chengshulow) & 0xFFFFFFFF) == targetv
) {
g_find_val_low = (ustartv + i);
g_finded_low = true;
}
if (g_finded_low)
break;
}
return 0;
}
std::uint32_t CalcThreadHigh(void * start_v) {
std::uint64_t ustartv = (std::uint64_t) start_v;
for (std::uint64_t i = 0; i < g_chunk_size; i++) {
std::uint64_t vv = ((ustartv + i) << 32) | (g_find_val_low);
if (
(vv * g_chengshu) == g_jieguo
) {
g_find_val_high = (ustartv + i);
g_finded_high = true;
}
if (g_finded_high)
break;
}
return 0;
}
std::uint64_t findchengshu(std::uint64_t jieguo, std::uint64_t chengshu) {
g_chengshu = chengshu;
g_jieguo = jieguo;
g_finded_low = 0;
g_find_val_low = 0;
g_finded_high = 0;
g_find_val_high = 0;
int heshu = 8;
std::uint64_t block_size = (0x100000000 / heshu);
g_chunk_size = block_size;
for (int i = 0; i < heshu; i++) {
std::uint32_t tid = 0;
CalcThread((void * )(block_size * i));
///CreateThread(0, 0, CalcThread, (void*)(block_size * i), 0, &tid);
}
while (g_finded_low == false)
sleep(10);
for (int i = 0; i < heshu; i++) {
std::uint32_t tid = 0;
CalcThreadHigh((void * )(block_size * i));
///CreateThread(0, 0, CalcThreadHigh, (void*)(block_size * i), 0, &tid);
}
while (g_finded_high == false)
sleep(10);
return g_find_val_low | (((std::uint64_t) g_find_val_high) << 32);
}
std::uint64_t reneg(std::uint64_t v) {
return ~v + 1;
}
std::uint64_t re22(std::uint64_t v) {
std::uint64_t _1 = v & 0xFF;
std::uint64_t _2 = (v & 0xFF00) >> 8;
std::uint64_t _3 = (v & 0xFFFFFF) >> 16;
std::uint64_t _4 = (v & 0xFFFFFFFF) >> 24;
std::uint64_t _5 = (v & 0xFFFFFFFFFF) >> 32;
std::uint64_t _6 = (v & 0xFFFFFFFFFFFF) >> 40;
std::uint64_t _7 = (v & 0xFFFFFFFFFFFFFF) >> 48;
std::uint64_t _8 = (v & 0xFFFFFFFFFFFFFFFF) >> 56;
return _2 | (_1 << 8) | (_4 << 16) | (_3 << 24) | (_6 << 32) | (_5 << 40) | (_8 << 48) | (_7 << 56);
}
std::uint64_t re15(std::uint64_t v) {
return ((v & 0x00FFFFFFFFFFFFFF) << 8) | (v >> 56);
}
std::uint64_t re9(std::uint64_t v) {
std::uint64_t nv = ((v >> 32) & 0xFFFFFFFF) | (v << 32);
return nv ^ 0xCE9A20C53746A9F7;
}
std::uint64_t invertVal(std::uint64_t v) {
v = reneg(v);
v = findchengshu(v, 0x51F6D71704B266F5);
v = v ^ 0xB9B8A788569D772D;
v = re22(v);
v -= 0x29D5CA44D143B4FC;
v ^= 0x326DEB9C5D995AEB;
v = re15(v);
v -= 0x18B205A73CB902B7;
v = findchengshu(v, 0xA648BD40DACE4EF5);
v = re9(v);
v -= 0x8BC715D20D923835;
v ^= 0xB31C9545AC410D72;
v = reneg(v);
v += 0x4DDB14EE5C8771C5;
v = ~v + 1;
return v;
}
std::uint64_t reval(std::uint64_t v) {
std::uint64_t _1 = v & 0xFF;
std::uint64_t _2 = (v & 0xFF00) >> 8;
std::uint64_t _3 = (v & 0xFFFFFF) >> 16;
std::uint64_t _4 = (v & 0xFFFFFFFF) >> 24;
std::uint64_t _5 = (v & 0xFFFFFFFFFF) >> 32;
std::uint64_t _6 = (v & 0xFFFFFFFFFFFF) >> 40;
std::uint64_t _7 = (v & 0xFFFFFFFFFFFFFF) >> 48;
std::uint64_t _8 = (v & 0xFFFFFFFFFFFFFFFF) >> 56;
return _8 | (_7 << 8) | (_6 << 16) | (_5 << 24) | (_4 << 32) | (_3 << 40) | (_2 << 48) | (_1 << 56);
}
int main() {
std::uint64_t val[9];
val[8] = 0;
val[0] = reval(invertVal(0x875cd4f2e18f8fc4));
val[1] = reval(invertVal(0xbb093e17e5d3fa42));
val[2] = reval(invertVal(0xada5dd034aae16b4));
val[3] = reval(invertVal(0x97322728fea51225));
val[4] = reval(invertVal(0x4124799d72188d0d));
val[5] = reval(invertVal(0x2b3e3fbbb4d44981));
val[6] = reval(invertVal(0xdfcac668321e4daa));
val[7] = reval(invertVal(0xeac2137a35c8923a));
printf("%s\n", val);
}
Conclusions
This challenge was interesting to discover other obfuscations, I have also learned other features from Triton, and I thought it was useful for a second post. I hope you have enjoyed the post and see you in the next one space cowboy!

